Математика: Решите уравнение -5x+16=26 4 (x-3 )-6=5x+7 9x-13=8+2x 8 (2x-3)+7=4 (2-x)-1

Решите уравнение -5x+16=26 4 (x-3 )-6=5x+7 9x-13=8+2x 8 (2x-3)+7=4 (2-x)-1

👇

Ответ:

ivan111111

27.02.2022

-5x+16=26
-5x=26-16
-5x=10
x=10:(-5)
x=-2

4 (x-3 )-6=5x+7
4x-12-6=5x+7
4x-18=5x+7
5x-4x=-18-7
x=-25

9x-13=8+2x
9x-2x=8+13
7x=21
x=21:7
x=3

8 (2x-3)+7=4 (2-x)-1
16x-24+7=8-4x-1
16x-17=7-4x
16x+4x=7+17
20x=24
x=24:20
x=1,2

4,6(58 оценок)

Ответ:

YakovlevaJulia2004

27.02.2022

1)
-5х+16=26
-5х=10
х=-2
ответ: -2.
2)
4(х-3)-6=5х+7
4х-12-6=5х+7
4х-5х=7+12+6
-х=25
х=-25
ответ: -25.
3)
9х-13=8+2х
9х-2х=8+13
7х=21
х=3
ответ: 3.
4)
8(2х-3)+7=4(2-х)-1
16х-24+7=8-4х-1
16х+4х=8-1+24-7
20х=24
х=1,2
ответ: 1,2

4,4(51 оценок)

Открыть все ответы

Ответ:

10672

27.02.2022

Из условия следует, что треугольник прямоугольный, далее, рассмотрим треугольник ACD. Все углы у него известны, а именно

^CAD = 15 (по условию)

^ACD = 45 (СD - биссектриса прямого угла)

^ADC = 120 (180-15-45)

и одна сторона тоже

АС = sqrt(3).

Следовательно, треугольник полностью определён и не представляет сложностей найти все другие его элементы.

Длину стороны AD проще всего найти из теоремы синусов

AD/sin(^ACD)=AC/sin(^ADC), откуда

AD =AC*sin(^ACD)/sin(^ADC), подставим исходные данные

AD = sqrt(3)*sin(45)/sin(180-60)=(sqrt(3)*sqrt(2)/2)/(sqrt(3)/2)=sqrt(2)

Вот и всё. Вроде так.

Подробнее - на -

Пошаговое объяснение:

4,6(6 оценок)

Ответ:

Alexsandar

27.02.2022

Задачу можно решить методом «научного тыка»

Допустим, в какой-то момент малыш Федя обгоняет Соню на ходулях. Отметим это место специальной меткой, как условное начало круга. Как только он обгоняет Соню, он понимает, что (теперь уже) она – впереди него на расстоянии длины круговой дорожки (фактически она почти впритык позади него, но ведь дорожка круговая (!), а значит, Соня, как бы и впереди на расстоянии длины дорожки).

Пускай теперь до нового места встречи Соня пройдёт от метки какую-то часть круговой дорожки, назовём это «кусок дорожки», а малыш Федя до этого нового места встречи проедет на велосипеде целый круг и ещё такую же часть дорожки, т.е. такой же «кусок», как и Соня.

Новое место встречи, таким образом, сместилось от начальной метки на «кусок дорожки».

После второй встречи, Федя опять обгонит Соню и потом опять встретится с ней уже в третий раз со смещением ещё на один «кусок дорожки» от предыдущего места встречи, которое и так уже было смещено от начальной метки на «кусок дорожки», стало быть, третья встреча сместится от начальной метки на «два куска дорожки».

Второе место встречи сместилось от начальной метки
на «кусок дорожки», а Федя проехал лишний круг.

Третье место встречи сместилось от начальной метки
на «два куска дорожки», а Федя проехал два лишних круга.

Четвёртое место встречи сместится от начальной метки
на «три куска дорожки», а Федя проедет три лишних круга.

Пятое место встречи сместится от начальной метки
на «четыре куска дорожки», а Федя проедет четыре лишних круга.

Заметим, что если бы Соня к пятому месту встречи, смещённому от начальной метки на «четыре куска дорожки бы целый круг, то тогда Федя проехал бы 4 лишних круга и ещё «четыре куска дорожки», т.е. такое же расстояние, как и Соня, а значит ещё один добавочный круг.

И в таком случае, получилось бы, что Соня один круг, а Федя проехал пять кругов, что как раз и сходится с их соотношением скорости. Всё правильно, Федя ведь ездит в 5 раз быстрее, а значит, он и должен проехать в 5 раз больше, чем проходит Соня!

Значит, наше предположение верно. К пятой встрече Соня проходит полный круг, а стало быть, она приходит к начальной метке, которую мы отметили в месте первой встречи, т.е. место пятой встречи совпадает с местом первой встречи. Дальнейшие встречи станут совпадать со встречами в первом цикле рассуждений. Таким образом, всего существует 4 разных места, где Федя обгоняет Соню.

Так же, эту задачу можно решить и «аналитически», через введение неизвестного параметра скорости, и рассмотрения относительной скорости участников, т.е. скорости сближения.

Пусть скорость Сони равна v .

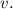Тогда скорость Феди равна 5v .

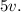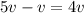Когда Федя догоняет Соню, их скорость сближения равна 5v - v = 4v

(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять).

Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения.

Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.

О т в е т : (б) в 4 точках.

4,8(35 оценок)

Это интересно:

Искусство-и-развлечения

26.03.2021

Как найти свой танцевальный стиль?...

Компьютеры-и-электроника

23.02.2021

Битмоджи на Facebook: Как произвести впечатление на своих друзей...

Стиль-и-уход-за-собой

04.06.2021

Избавляемся от перхоти натуральными средствами...

Стиль-и-уход-за-собой