Площадь боковой поверхности - 84 см²; площадь полной поверхности 12(√3 + 7) ≈ 104,78 см²
Пошаговое объяснение:
1) Площадь одного основания s найдём как площадь двух треугольников со сторонами 3 и 4 см (то есть рассматриваем площадь параллелограмма как сумму площадей двух равных треугольников):
s = 2 · (3 · 4 · sin 60° / 2) = 12 · √3/2 = 6√3 см².
В прямом параллелепипеде таких оснований 2.
Соответственно площадь двух оснований равна произведению площади одного основания s на 2:
S осн = s · 2 = 6√3 · 2 = 12 √3 см².
2) Воспользовавшись теоремой косинусов, найдём меньшую диагональ основания d. Меньшей является та диагональ, которая лежит против угла 60°, а большая диагональ лежит против угла 120° (этот угол мы находим, исходя из свойства параллелограмма: сумма углов, прилежащих к одной стороне, равна 180°):
d² = 3² + 4² - 2· 3 · 4 · cos 60° = 9 +16 - 24 · 0,5 = 25 - 12 = 13
d = √13.
3) Меньшей диагонали основания соответствует и меньшая диагональ параллелепипеда, которые вместе с высотой образуют прямоугольный треугольник, в котором диагональ параллелепипеда является гипотенузой. По теореме Пифагора находим высоту H:
H = √(7² - (√13)²) = √(49 - 13) = √36 = 6 см
4) Площадь боковой поверхности S бок прямого параллелепипеда равна произведению периметра его основания P на высоту H:
Р = (3 + 4) · 2 = 7 · 2 = 14 см
S бок = P · H = 14 · 6 = 84 cм²
5) Площадь полной поверхности S прямого параллелепипеда:
S = S осн + S бок = 12√3 + 84 = 12 · (√3 + 7) ≈ 12 · ( 1,732 + 7) = 12 · 8,732 ≈ 104,78 см²
ответ: площадь боковой поверхности - 84 см²; площадь полной поверхности 12(√3 + 7) ≈ 104,78 см²
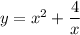
Для начала найдём область определения функции.
1) 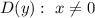
Определим, является эта функция чётной, нечётной или же ни чётной, ни нечётной.
2) 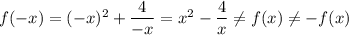 - следовательно, функция не является ни чётной, ни нечётной.
- следовательно, функция не является ни чётной, ни нечётной.
Найдём точки пересечения с осью Ox (y = 0).
3)
![y = 0\\\\x^2 + \dfrac{4}{x} = 0\\\\\\\dfrac{x^3+4}{x} = 0\\\\\\x^3 + 4 = 0\\\\x^3 = -4\\\\\boxed{x = -\sqrt[3]{4}}](/tpl/images/1672/7765/c3fb8.png)
Найдём точки пересечения с осью Oy (x = 0).
4) Так как x ≠ 0 (см. область определения), то точек пересечения графика функции с осью Oy нет.
Найдём промежутки знакопостоянства.
5)
+ - +
-----------------------о-----------------------о-----------------------> x
![-\sqrt[3]{4}](/tpl/images/1672/7765/da371.png)
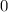
Функция положительна при ![x\in \left(-\infty;\ -\sqrt[3]{4}\right);\ (0;\ +\infty)](/tpl/images/1672/7765/1a568.png) .
.
Функция отрицательна при ![x\in \left(-\sqrt[3]{4}\ ;\ 0\right)](/tpl/images/1672/7765/405d9.png) .
.
Найдём асимптоты графика функции.
6) вертикальная асимптота: 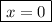 .
.
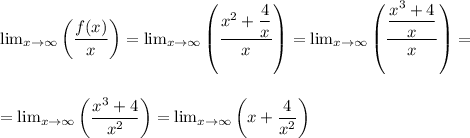
Предел равен 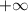 . Горизонтальных асимптот не существует, наклонных асимптот не существует.
. Горизонтальных асимптот не существует, наклонных асимптот не существует.
Вычислим производную и найдём критические точки функции.
7)
![y' = \left(x^2\right)' + \left(\dfrac{4}{x}\right)' = 2x - \dfrac{4}{x^2} = \boxed{\dfrac{2x^3 - 4}{x^2}}\\\\\\y' = 0\\\\\dfrac{2x^3 - 4}{x^2} = 0\\\\2x^3 - 4 = 0\\\\2x^3 = 4\\\\x^3 = 2\\\\\boxed{x = \sqrt[3]{2}}](/tpl/images/1672/7765/e0325.png)
Найдём промежутки монотонности функции, точки экстремума и значение функции в этих точках.
8)
- - + f'(x)
----------------------о------------------ ---------------------------------> x
---------------------------------> x
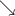
![\sqrt[3]{2}](/tpl/images/1672/7765/f1dc1.png)
 f(x)
f(x)
Функция убывает при ![x\in \left(-\infty;\ 0);\ \left(0;\ \sqrt[3]{2}\ \right]](/tpl/images/1672/7765/b3681.png) .
.
Функция возрастает при ![x \in \left[\sqrt[3]{2}\ ;\ +\infty\right)](/tpl/images/1672/7765/2f042.png) .
.
![\sqrt[3]{2}](/tpl/images/1672/7765/f1dc1.png) - точка минимума функции.
- точка минимума функции.
![y\left(\sqrt[3]{2}\ \right) = \left(\sqrt[3]{2}\right)^2 +\dfrac{4}{\sqrt[3]{2}} = \sqrt[3]{4}\ + 2\sqrt[3]{4} = \boxed{3\sqrt[3]{4}}](/tpl/images/1672/7765/0dd6b.png) .
.
Вычислим вторую производную.
9) 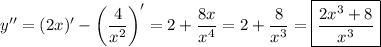
Определим выпуклость функции и найдём точки перегиба.
10)
![y'' = 0\\\\\dfrac{2x^3 + 8}{x^3} = 0\\\\2x^3 + 8 = 0\\\\2x^3 = -8\\\\x^3 = -4\\\\x = -\sqrt[3]{4}](/tpl/images/1672/7765/fb9d6.png)
+ - +
-----------------------о-----------------------о-----------------------> x
![-\sqrt[3]{4}](/tpl/images/1672/7765/da371.png)
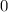
Функция выпукла вниз при ![x\in \left(-\infty;\ -\sqrt[3]{4}\right);\ (0;\ +\infty)](/tpl/images/1672/7765/1a568.png) .
.
Функция выпукла вверх при ![x\in \left(-\sqrt[3]{4}\ ;\ 0\right)](/tpl/images/1672/7765/405d9.png) .
.
Точка перегиба: ![-\sqrt[3]{4}](/tpl/images/1672/7765/da371.png) .
.
Определим множество значений функции.
11) 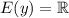 .
.
x:2-12+5=6
x:2=6+12-5
x:2=13
x=2×13
x=26
ответ:26 задумали