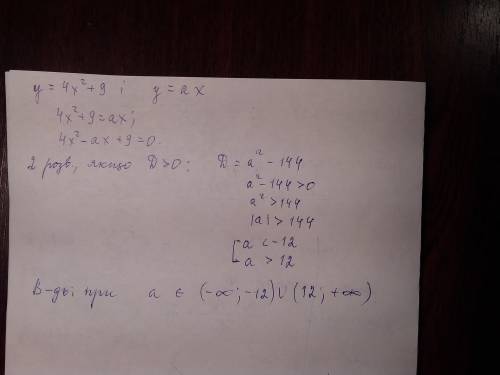ответ: Е( у ) = [ 3 ; 6 ] .
Пошаговое объяснение:
y = 6sin⁴x+6cos⁴x . Перетворимо функцію :
y = 6sin⁴x+6cos⁴x = 6(sin⁴x + cos⁴x ) = 6(sin⁴x + 2sin²xcos²x + cos⁴x -
- 2sin²xcos²x ) = 6(sin⁴x + 2sin²xcos²x + cos⁴x ) - 12sin²xcos²x =
= 6 ( sin²x + cos²x )² - 3 ( 4sin²xcos²x ) = 6 * 1² - 3*sin²2x = 6 - 3sin²2x =
= 6 - 3( 1 - cos4x )/2 = 6 - (3 - 3cos4x )/2 = ( 12 -3 + 3cos4x )/2 =
= ( 9 + 3cos4x )/2 ; отже , дана функція y = ( 9 + 3cos4x )/2 .
Оцінимо її значення : - 1 ≤ сos4x ≤ 1 ;│X 3
- 3 ≤ 3cos4x ≤ 3 ; │+ 9
9 - 3 ≤ 9 + 3cos4x ≤ 9 + 3 ;
6 ≤ 9 + 3cos4x ≤ 12 ; │: 2
6 : 2 ≤ ( 9 + 3cos4x )/2 ≤ 12 : 2 ;
3 ≤ y ≤ 6 .
Таким чином , множина значень даної в умові функції Е( у ) = [ 3 ; 6 ] .
a∈(-∞;-12)∪(12;+∞)
Пошаговое объяснение:
Приравняем 4x²+9 и ax (т.к. речь об общих точках двух функций)
4x²+9=ax
Перенесём всё в левую часть
4x²+9-ax=0
4x²-ax+9=0
Получаем уравнение вида ax²+bx+c=0
Значения x -- это корни уравнения и точки пересечения.
Но количество корней квадратного уравнения определяется дискриминантом. Чтобы уравнение имело 2 корня, дискриминант должен быть больше нуля.
Сначала находим дискриминант получившегося уравнения:
D=(-a²)-4·4·9= a²-144
Дискриминант должен быть больше нуля:
a²-144>0
Решим квадратное неравенство
a²-144=0
a²=144
a1=12
a2= -12
Схематично изображаем параболу, пересекающую ось в точках 12 и -12(Прикрепляю фото)
В промежутках (-∞;-12)∪(12;+∞) a больше нуля.
Значит, ответ a∈(-∞;-12)∪(12;+∞)