400
Пошаговое объяснение:
Требуется вычислить сумму
S = 1 + 3 + 5 + ... + 35 + 37 + 39
Количество слагаемых равно (39-1):2+1=38:2+1=19+1=20.
Первый член арифметической прогрессии a₁=1, разность d=2. Нужно вычислить сумму первых n=20 членов прогрессии. Так как последний член прогрессии a₂₀=39, то можно использовать формулу
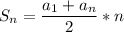 .
.
Тогда
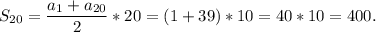
Перепишем сумму в двух видах
S = 1 + 3 + 5 + ... + 35 + 37 + 39
S = 39 + 37 + 35 + ... + 5 + 3 + 1
Так как количество слагаемых 20, то сумма обоих сумм равна
2·S = (1+39)+(3+37)+(5+35)+ ... +(5+35)+(3+37)+(1+39) =
=40+40+40+...+40+40+40=40·20
или
S = 40·20:2= 800:2=400.
Объяснение:
Ряды "8". Ряды "7"
8 плиток - полный ряд "8" 1 ряд "7"+1 во втором ряду.
16 плиток 2 полных ряда "8" 2 ряда "7" +2 в третьем ряду
и так далее ... .
В неполном ряду "7" должно быть + 6 плиток. В неполном ряду "8" +1 плитка. Тогда выполняется условие 6-1=5
7*5=35+6= 41 плитка
8*5=40+1= 41 плитка
Всё логично и понятно.
Есть второй ответ - 97 плиток.
Решается через неравенство 7а+6<100; a <13,4; отсюда, а=13, 13*7+6=97, проверка: 12*8+1=97
Все условия задачи, в том числе ограничение в 100 плиток выполнены.