Дано
Площадь одной плитки = 400:
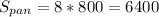
Найти к-во Q потребующихся для замощения панели плиток
Решение
Нужно разделить пл. всей панели на пл. 1 плитки:
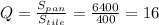
ответ 16
Задача 2Дано
Периметр прямоугольника (Prec) = 120. У прямоугольника противоположные стороны равны. Сторона a = b + 10 Сторона b = x (тогда a = x + 10)Найти площадь прямоугольника Srec
Решение
Исходя из формулы нахождения P прямоугольника, имеем
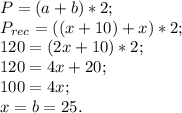
Мы нашли длину стороны b. Отсюда находим сторону a:
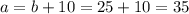
Площадь прямоугольника Srec является произведением длин его сторон:
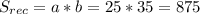
ответ 875 кв. см
Задача 3Купил тетрадей на сумму 8 (шт) * 25 (тг) = 200 (тг),купил ручек на сумму 3 (шт) * 120 (тг) = 360 (тг).ответ: всего потратил 200 + 360 = 560 тг.
Задача 4Дано
Прямоугольник j,его сторона a = 7,его периметр P = 40Найти сторону b
По формуле периметра прямоугольника получаем формулу для нахождения стороны b:
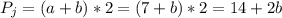
Периметр известен, подставляем его значение в формулу и находим b:
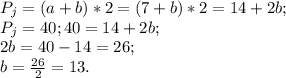
ответ 13
Задача 5Дано
Квадрат с периметром 36 см
Найти его площадь
Решение
Площадь квадрата – это, как бы неловко ни звучало, квадрат его одной стороны.
Введём переменную для стороны квадрата – a. Зная, что стороны квадрата равны, а их 4, работаем с первой известной нам из "Дано" переменной – с периметром. По формуле нахождения периметра квадрата получаем, что сторона a = 9:
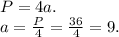
Второй и последний шаг – площадь квадрата. Значения всех необходимых переменных нам теперь известны (сторона):
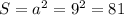
ответ 81 кв. см
ответ: нет . Более того , невозможно получить произвольное натуральное число N.
Пошаговое объяснение:
Найдем среди чисел от 2 жо 1994 число содерщащее в делителях максимальную степень двойки.
Такое число единственно и равно : 2^10=1024
Предположим , что произвольная комбинация + ,- из слагаемых :
1/2 ;1/3 ; 1/4 1/994 равна натуральному числу N.
Тогда умножим обе части равенства на 2^10.
Во всех дробях вида : 2^10/k сократяться со знаменателем все степени числа 2, что содержит число k. (То есть знаменатели всех дробей станут нечетными) . Если число k отлично от 2^10 , то числители этих дробей будут четны , тк все эти числа содержат в себе меньше чем 2^10.
Но если число k=2^10=1024 , то это единственное число которое после сокращения имеет нечетный числитель равный 1. Другими словами это будет просто число 1 (2^10/2^10)=1.
Всего от 2 до 1994 : 1993 числа , одно из которых равно единице , а остальные имеют четные числители и нечетные знаменатели.
Если перенести единицу в правую часть равенства , то получим cправа:
2^10*N +-1 - абсолютно очевидно , что число справа является нечетным. (+- в зависимости от того какой знак стоит перед ним)
А слева у нас остается 1992 числа с четными числителями и нечетными знаменателями. Если привести каждую из данных дробей к общему нечетному знаменателю ( тк общий знаменатель нечетных чисел число нечетное) , то получим дробь с нечетным знаменателем и числителем состоящим сумм и разностей четных чисел. ( Cумма или разность в любых комбинациях произвольного числа четных чисел число четное)
Таким образом получаем :
A/B= 2^10 *N+-1=C
A-четное число
B-нечетное число
2^10*N +-1=C -нечетное число
Но тогда :
A=B*C -то есть мы получили, что произведение двух нечетных чисел равна четному числу. Мы пришли к противоречию.
Нельзя расставить знаки «+». «-» между дробями 1/2,1/3,1/4...1/1994 так , чтобы в результате получилось натуральное число. Cоответственно число 4 не является исключением из правил и его так же получить невозможно.
а = с/b,
периметр:
Р = 2*(а + b) = 2*(с/b + b)