4. Из основного тригонометрического тождества:
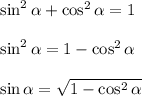
Так как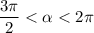 
, то 
.
.
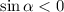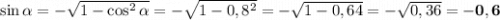ответ: -0,6
5.
![\sqrt[6]{\left(m-n\right)^6} - \sqrt[4]{m^4} = \left|m-n\right| - \left|m\right|](/tpl/images/1874/3421/381cf.png)
Так как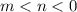 
, то модуль будет раскрываться вот так:
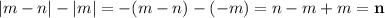
ответ: n
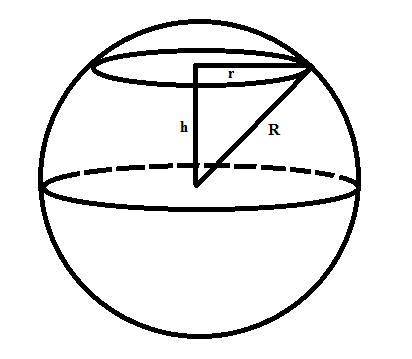
6. (см. чертёж во вложении) Сечение шара представляет собой круг. Площадь круга задаётся формулой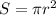 
, отсюда:
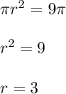
Получается прямоугольный треугольник, где гипотенуза - это радиус шара, один катет - радиус сечения, второй катет - расстояние от центра шара до сечения. По теореме Пифагора:
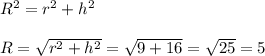
Формула объёма шара: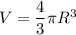 
. Подставляем известные значения:
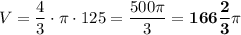
ответ: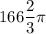 
7.
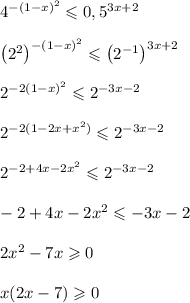
Решим неравенство методом интервалов.
Нули: 0; 3,5
+ - +
--------------------
----------------------------------------> x
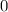
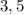
Так как в последней строке неравенства стоит знак "больше или равно", нам подходят те промежутки, где стоит знак "плюс".
ответ: ![x\in\left(-\infty;\ 0\right]\cup\left[3,5;+\infty\right)](/tpl/images/1874/3421/1b59b.png)
.
Первому 130 руб.,
Второму 40 руб.
Пошаговое объяснение:
Не совсем корректное условие.
При принесенной Третьим сумме 160 рублей задача четкого решения не имеет.
Но - если Третий отдал 170 рублей, задачу можно решить, если сделать следующие допущения:
- мальчики, что принесли пирожки, взяли их в том числе и с учетом доли третьего.
- принесенные 10 пирожков и 7 пирожков делятся поровну, каждому достается своя доля,
- принесенные третьим 170 руб - плата третьего, отданная за свою долю пирожков, а значит,
- деньги должны поделить между собой только двое - первый и второй.
Итак, 170 руб можно расценивать как оплату за одну долю ужина из пирожков - назовем ее стоимость доли (СД)
Всего едоков - 3 человека. Следовательно, можно оценить "Общую стоимость ужина" (ОС) как:
ОС = 3 (чел) • СД = 3•170 = 510 руб.
А пирожков всего было:
10 + 7 = 17 (пирожков)
Значит, стоимость 1 пирожка равна
510 : 17 = 30 (руб/пирожок)
Отсюда:
Первый купил 10 пирожков, на сумму
30 • 10 = 300 (руб)
Второй купил 7 пирожков, на сумму
30 • 7 = 210 (руб)
И каждый сам съел пирожков на 170 рублей, а значит
Первый переплатил
300 - 170 = 130 (руб)
Второй переплатил
210 - 170 = 40 (руб)
А это значит, что деньги нужно поделить так:
Первому 130 руб,
Второму 40 руб
2)360:6=60Г
1)90:15*2=12
1)?