Производной функции y=5x^6 являеться производной y=x^2-3x-1/x^2 является производной является y=1/3x^5

👇

Увидеть ответ

Ответ:

mahin2

10.06.2020

Рпопгпнананагпшпеппипгнн

4,6(71 оценок)

Открыть все ответы

Ответ:

dvofgisf

10.06.2020

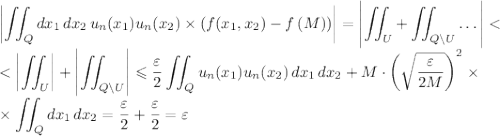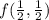
$f(\frac12,\frac12)$

Пошаговое объяснение:

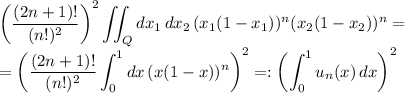
$\displaystyle \left(\frac{(2n+1)!}{(n!)^2}\right)^2\iint_Qdx_1\,dx_2\,(x_1(1-x_1))^n(x_2(1-x_2))^n=\\=\left(\frac{(2n+1)!}{(n!)^2}\int_0^1 dx\, (x(1-x))^n\right)^2=:\left(\int_0^1 u_n(x)\,dx\right)^2$

Выражение в скобках равно 1, достаточно n раз проинтегрировать по частям:

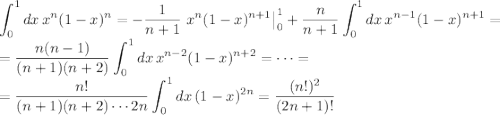
$\displaystyle \int_0^1 dx\, x^n(1-x)^n=-\frac1{n+1}\left.x^n(1-x)^{n+1}\right|_0^1+\frac n{n+1}\int_0^1dx\, x^{n-1}(1-x)^{n+1}=\\=\frac{n(n-1)}{(n+1)(n+2)}\int_0^1dx\,x^{n-2}(1-x)^{n+2}=\dots=\\=\frac{n!}{(n+1)(n+2)\cdots2n}\int_0^1 dx\,(1-x)^{2n}=\frac{(n!)^2}{(2n+1)!}$

Тогда

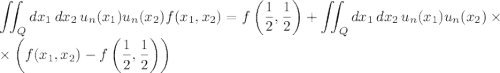
$\displaystyle\iint_Qdx_1\,dx_2\,u_n(x_1)u_n(x_2) f(x_1,x_2)=f\left(\frac12,\frac12\right)+\iint_Qdx_1\,dx_2\,u_n(x_1)u_n(x_2)\times\\\times\left(f(x_1,x_2)-f\left(\frac12,\frac12\right)\right)$

Значение интеграла стремится к нулю: функции 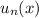u_n(x) быстро уменьшаются при отдалении от 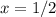x=1/2 , а вблизи точки 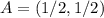A=(1/2,1/2) разность значений функций мала ввиду непрерывности f.

Более формально:

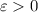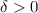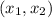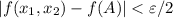
1. Функция f непрерывна, поэтому для любого $\varepsilon0$ найдётся такая $\delta0$ , что для всех (x_1,x_2) из $U=[1/2-\delta,1/2+\delta]^2$ выполнено неравенство |f(x_1,x_2)-f(A)|

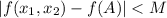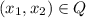2. Функция f непрерывна на компакте Q, тогда она ограничена на Q. Тогда найдётся число M > 0, для которого |f(x_1,x_2)-f(A)| при всех $(x_1,x_2)\in Q$ .

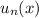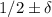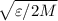3. Очевидно, максимум функции u_n(x) на множестве $[0,1]\backslash[1/2-\delta,1/2+\delta]$ достигается в точках $1/2\pm\delta$ . Покажем, что при возрастании n он становится сколь угодно малым (в частности, найдётся такое N, что при всех n > N максимум будет меньше $\sqrt{\varepsilon/2M}$ ).

Формула Стирлинга позволяет получить асимптотику для коэффициента с факториалами:

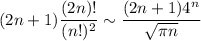
$(2n+1)\dfrac{(2n)!}{(n!)^2}\sim\dfrac{(2n+1)4^n}{\sqrt{\pi n}}$

Тогда максимум при больших n будет «примерно»

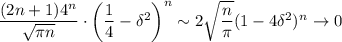
$\dfrac{(2n+1)4^n}{\sqrt{\pi n}}\cdot\left(\dfrac14-\delta^2\right)^n\sim2\sqrt{\dfrac{n}{\pi}}(1-4\delta^2)^n\to 0$

Собираем вместе: для любого 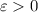$\varepsilon0$ найдётся такое N, что при всех n > N

$\displaystyle\left|\iint_Qdx_1\,dx_2\,u_n(x_1)u_n(x_2)\times\left(f(x_1,x_2)-f\left(M\right)\right)\right|=\left|\displaystyle\iint_U+\iint_{Q\backslash U}\dots\right|$

4,5(94 оценок)

Ответ:

Sasha2771

10.06.2020

1 234 567 890. У нас 10-тичная запись чисел. Мы используем только 10 цифр. Но при их можем записать любое, даже очень большое число. Число зависит не только от цифр, но и от места, где они стоят.
25 и 52, цифры одинаковые, а числа разные. На первом справа месте стоят единицы, на втором десятки. В числе 25 только 2 десятка, в 52 - 5 десятков, оно больше. В твоем числе 0 единиц, 9 десятков (ответ на 1) вопрос). На 3 месте сотни. В нашем числе 8 сотен. 300 - число, в котором 3 сотни, а десятков и единиц нет. Единицы, десятки и сотни - 1класс ЕДИНИЦ. Первые три места, а правильно разряда, занимают ЕДИНИЦЫ. Дальше на фото.
Instagramm @neznaikaqvera не понимает этого : дано число 1234567890. какая цифра записана в разряде: