(см. объяснение)
Пошаговое объяснение:
Вынесении общего множителя за скобки.
Рассмотрим пример:
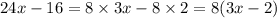
Хорошо видно, что и 24 и 16 делятся на 8. Тогда 8 - это общий множитель, который можно вынести за скобки. Далее делим исходное выражение на 8 и отправляем полученное в скобки.
Попробуйте решить самостоятельно:
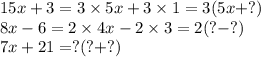
(ответы в конце объяснения)
Вынесении многочлена за скобки:
Прием тут аналогичен описанному выше.
Рассмотрим пример:
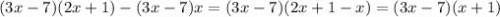
Здесь все то же самое, только за скобки выносится общая часть.
При этом не нужно бояться выражения в скобках!
Если оно одинаково, то смело пользуйтесь приемом:
![(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x})-(\sqrt[7]{x}+\arcsin (x))^2=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x}-(\sqrt[7]{x}+\arcsin (x)))=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)-\arcsin (x))](/tpl/images/1643/8776/95ae2.png)
Каким бы страшным не показалось семикласснику это выражение, прием остается 100% таким же!
Группировка.
Рассмотрим пример:
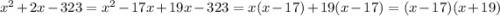
Здесь необходимо представить 2x, как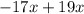 
. После чего воспользоваться знаниями выше.
Иногда сразу дают выражение вида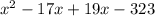 
, что упрощает ситуацию.
ответы к заданиям для самостоятельного решения.
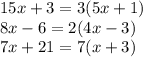
Объяснение завершено!
Искомые три числа обозначим через a, b и c. Согласно первого условия задания: a : b = 4 : 9. Второе условие позволит написать b : c = 15 : 22/3. Третье условие оформим как a + b + c = 219. Таким образом, получили три уравнения с тремя неизвестными.
Решим эту систему трёх уравнений. К первым двум уравнениям применим основное свойство пропорции. Тогда они примут вид: 9 * а = 4 * b; (22/3) * b = 15 * c или а = (4/9) * b; b = 15 * c / (22/3) = 15 * с * (3/8) = (45/8) * с = 5,625 * с. Выразим а через с. Имеем: а = (4/9) * (45/8) * с = ((4 * 45) / (9 * 8)) * с = 2,5 * с.
Подставим найденные выражения в последнее уравнение: 2,5 * с + 5,625 * с + с = 219 или (2,5 + 5,625 + 1) * с = 219, откуда с = 219 : 9,125 = 24. Тогда, а = 2,5 * 24 = 60 и b = 5,625 * 24 = 135.
ответ: 60; 135; 24.
