Расстояние меж пристанями равно 225 километров.
Пошаговое объяснение:
учитывая что скорость катера постоянна, получается что ему предстоит пройти еще две части пути до пристани.
значит еще два раза по три часа, и того получается 9 часов пути со скорость 25 км\ч.
Запишем всё это в числах:
S - это расстояние
расстояние поделили на три части условием задачи
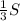 (км) катер за 3 часа
(км) катер за 3 часа
тогда S (км) катер за 9 часов (домножили на три обе части)
расстояние мы находим по формуле "S=V*t"
S - расстояние (км)
V - скорость (км\ч)
t - время (ч)
S = 9*25 = 225км
ответ №1:
№1 1)24000/80=300
2)300/20=15
3)561/17=33
4)726/11=66
5)300-15=285
6)285+33=318
7)318+66=384
№2 1)24000/80-300=0
2)0/20=0
3)561/17+726=759
4)759/11=69
№3 1)395*72-603=27837
2)27837*16=445392
3)960/24=40
4)445392-40=445352
№4 1)395*72=28440
2)603*16=9648
3)960/24=40
4)28440-9648-40=18752
ответ №2:
1)24000: 80-300: 20+561: 17+726: 11=300-15+33+66=384
а)24000: 80=300 д)300-15=285
б)300: 20=15 е)285+33=318
в)561: 17=33 ж)318+66=384
г)726: 11=66
2) (24000: 80-300): 20+(561: 17+726): 11=0+69=69
а)24000: 80=300 б)561: 17=33
300-300=0 33+726=759
0: 20=0 759: 11=69
3)(395*72-603)*16-960: 24=445352
а)395*72-603=28440-603=27837
б)27837*16=445392в)960/24=40г)445392-40=445352
4) 395*72-603*16-960: 24=28440-9648-40=18752
а)395*72=28440б)603*16=9648в)960/24=40
x^2 - 2x = x(x - 2) = 0; x1 = 0; x2 = 2
Если x <= 0 или x >= 2, то x^2 - 2x >= 0; |x^2 - 2x| = x^2 - 2x
Если 0 < x < 2, то x^2 - 2x < 0; |x^2 - 2x| = 2x - x^2
Если y < 0, то |y| = -y. Если y >= 0, то |y| = y.
Получаем 4 разных системы
1) x ∈ (-oo; 0] U [2; +oo); y ∈ (-oo; 0)
{ x^2 - 2x + y = 1
{ x^2 - y = 1
Приравниваем левые части
x^2 - 2x + y = x^2 - y
-2x = -2y
x = y
Подставляем во 2 уравнение
x^2 - x - 1 = 0
D = 1 - 4(-1) = 5
x1 = (1 - √5)/2 < 0 - подходит
x2 = (1 + √5)/2 > 0 - не подходит
Решение: x1 = y1 = (1 - √5)/2
2) x ∈ (0; 2); y ∈ (-oo; 0)
{ 2x - x^2 + y = 1
{ x^2 - y = 1
Выразим y в обоих уравнениях
{ y = x^2 - 2x + 1 = (x - 1)^2
{ y = x^2 - 1 = (x - 1)(x + 1)
Приравниваем правые части
(x - 1)^2 = (x - 1)(x + 1)
x1 = 1 ∈ (0; 2) - подходит; y = (x - 1)^2 = 0 - не подходит. Это НЕ решение.
x - 1 = x + 1 - решений нет.
Решений нет.
3) x ∈ (-oo; 0] U [2; +oo); y ∈ [0; +oo)
{ x^2 - 2x + y = 1
{ x^2 + y = 1
Подставляем 2 уравнение в 1 уравнение
1 - 2x = 1
x = 0 - подходит.
y = 1 - x^2 = 1 - 0 = 1 > 0 - подходит
Решение: x2 = 0; y2 = 1
4) x ∈ (0; 2); y ∈ [0; +oo)
{ 2x - x^2 + y = 1
{ x^2 + y = 1
Выразим y в обоих уравнениях
{ y = x^2 - 2x + 1 = (x - 1)^2
{ y = 1 - x^2 = (1 - x)(1 + x) = -(x - 1)(1 + x)
Приравниваем правые части
(x - 1)^2 = -(x - 1)(1 + x)
x = 1 ∈ (0; 2) - подходит, y = 1 - x^2 = 0 ∈ [0; +oo) - подходит
x - 1 = -1 - x; 2x = 0; x = 0 ∉ (0; 2) - не подходит
Решение: x3 = 1; y3 = 0
ответ: ((1 - √5)/2; (1 - √5)/2); (0; 1); (1; 0)