Пошаговое объяснение:
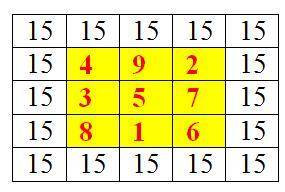
Магический квадрат – это квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу. Например (см. рисунок 1): таблица состоит из различных цифр от 1 по 9 и сумма чисел равна 15.
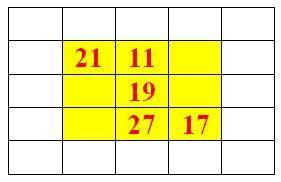
Другой пример (см. рисунок 2): даны всего 4 числа и нужно определить другие неизвестные числа и магический квадрат.
Для решение задачи сначала определим по известным 3 числам, в нашем примере, по числам диагонали определим сумму чисел: 21+19+17=57. Можно было определить нужную сумму чисел по известным 3 числам 2-столбца: 11+19+27=57.
Теперь нам известна сумма чисел и поэтому с её и 2 известных чисел можем определить неизвестные числа 1-строки и 3-строки:
57-21-11=25
57-27-17=13.
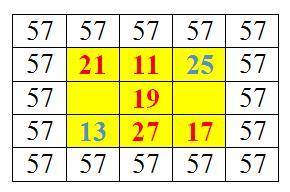
По известным уже числам 25 и 13 получаем другую таблицу (см. рисунок 3). Как видно из таблицы, остается найти неизвестных чисел 1-столбца и 3-столбца. Как и выше, определим их по числам столбца и с суммы:
57-21-13=23
57-25-17=15.
В итоге получаем нужную таблицу (см. рисунок 4). Можно проверить, что суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны 57.

2sin^2(x)-sqrt3*sin(x)=0
Sin(x)*(2sin(x)-sqrt3)=0
а)Либо sin(x)=0
б)Либо sin(x)=sqrt3/2
а)В первом случае x=pi*k, где k принадлежит целым
б)Во втором случае x=pi/6+2*pi*k
x=5*pi/6+2*pi*k
Дальше делаем выборку
Начиная с наим.
x=-10pi/3
x=-3pi
x=-2pi