В XIII−XIV веках город Кырым, или Солхат, был центром юрта (административной единицы) Золотой орды. По нему Крымом стали называть весь полуостров. Это был богатый торговый город, управляемый и частично населённый мусульманами, с большим количеством жителей-христиан — армян, греков, и итальянцев, богатевший на транзите восточных товаров из генуэзских портов — Кафы и Солдайи — на Русь, в Европу, и обратно.
В 1314 году, в начале правления хана Золотой орды Узбека, в Солхате была заложена мечеть. В 1332 году к ней добавили медресе по инициативе богатой женщины Инджибек-хатун, которая там же рядом в 1371 году была похоронена. Медресе на сегодняшний день представляет собой величественные руины, но мечеть сохранилась полностью.
Форма мечети простая, прямоугольная, крыша двухскатная. Минарет один, сбоку от входа. Портал и михраб украшены резьбой и надписями, в которых зафиксирована дата строительства. Мечеть действующая, но регулярно посещается туристами.
Рівняння вигляду 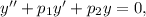 де
де 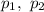 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді 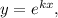 де
де 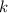 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 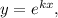 то
то 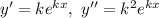
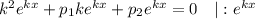
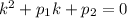 — характеристичне рівняння
— характеристичне рівняння
Можливі три випадки:
➀ 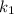 і
і 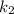 — дійсні,
— дійсні, 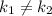
Фундаментальна система розв'язків: 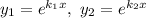 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 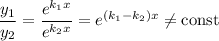
Загальний розв'язок: 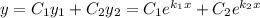
Приклад: а) 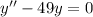
Метод Ейлера: 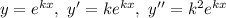
Характеристичне рівняння: 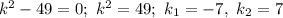
Загальний розв'язок: 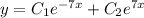
Відповідь: 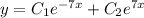
Приклад: в) 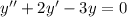
Метод Ейлера: 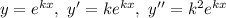
Характеристичне рівняння: 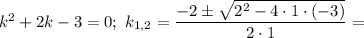
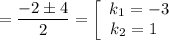
Загальний розв'язок: 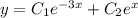
Відповідь: 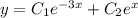
➁ 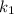 і
і 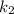 — дійсні,
— дійсні, 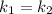
Якщо покласти 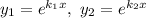 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 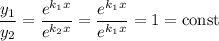
Фундаментальна система розв'язків: 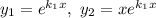 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 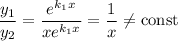
Загальний розв'язок: 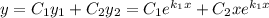
➂ 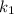 і
і 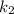 — комплексно спряжені,
— комплексно спряжені, 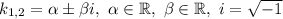
Фундаментальна система розв'язків: 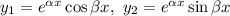 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 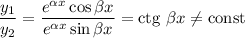
Загальний розв'язок: 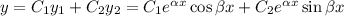
Приклад: б) 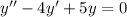
Метод Ейлера: 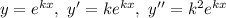
Характеристичне рівняння: 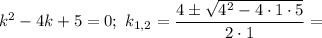
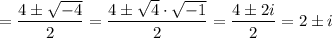
Отже, 
Загальний розв'язок: 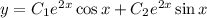
Відповідь: 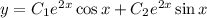
1) 15 1/3 - 8 5/18=15 6/18 - 8 5/18=7 1/18
2) 7 1/18 * 2 4/7=127/18 * 18/7=18 1/7
3) 18 1/7 : 6 1/21=127/7 * 21/127=3
4) 3 - 2 5/8=3/8