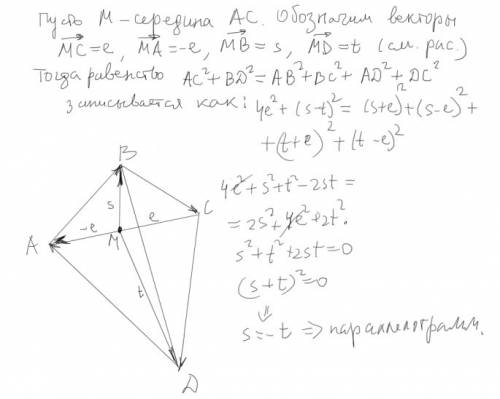
Log129 + 2 * log124 = 2.
Пошаговое объяснение:
Упростим (по возможности, и вычислим) данное логарифмическое выражение, которого обозначим через L = Log129 + 2 * log124, хотя об этом явного требования в задании нет. Анализ данного выражения показывает, что выражение L представляет собой сумму двух слагаемых, в каждом из которых участвует логарифмическое выражение, причем в обоих логарифмах основание одно и то же число 12.
Ко второму слагаемому применим формулу logabn = n * logab (где а > 0, a ≠ 1, b > 0, n – любое число). Тогда, оно примет вид: log1242 = log1216. Следовательно, имеем: L = Log129 + log1216.
К полученной сумме логарифмов применим формулу loga(b * с) = logab + logaс (где а > 0, a ≠ 1, b > 0, c > 0). Тогда, имеем: L = Log12(9 * 16) = Log12144.
Согласно определения логарифма, логарифм числа 144 по основанию 12 равен показателю степени, в которую нужно возвести 12, чтобы получить 144. Очевидно следующее: чтобы получить 144, число 12 нужно возвести в квадрат, то есть во вторую степень, другими словами, 122 = 144. Это означает, что log12144 = 2.
Предположим противное, то есть то, что Вася всегда сможет выписать очередное число. В силу попарного различия выписываемых чисел, их множество неограниченно.
Рассмотрим первые 9 чисел. Пусть у них есть общий делитель 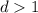 . Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель
. Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель 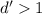 . Если при этом
. Если при этом 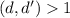 , то можно взять первые 10 чисел и у них окажется общий делитель
, то можно взять первые 10 чисел и у них окажется общий делитель 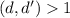 , противоречие. Значит,
, противоречие. Значит, 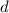 и
и 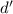 взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.
взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.