5
Пошаговое объяснение:
Я придумал вот что:
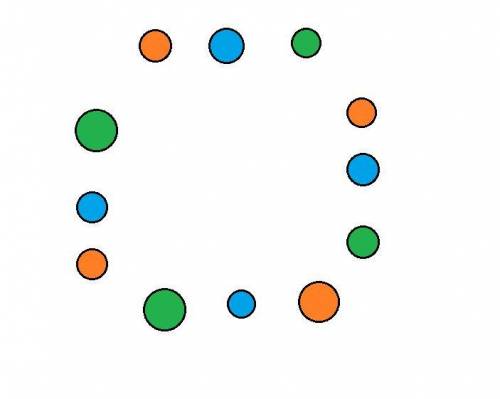
Раскрасим вершины (см. рисунок 1)
Нельзя выбирать больше 2-х одноцветных вершин, иначе эти 3 одноцветные вершины образуют равнобедренный треугольник.
Значит, всего вершин можно выбрать не более 6.
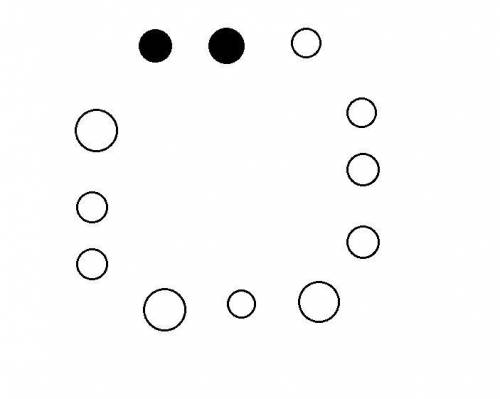
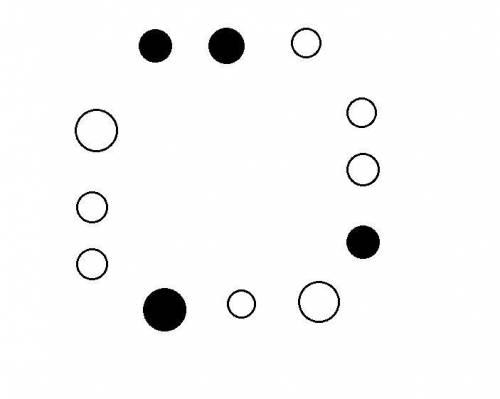
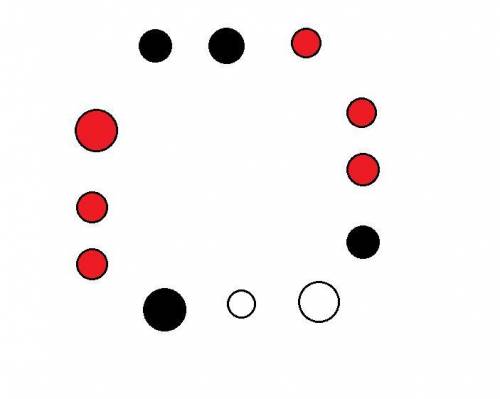
Предположим, можно выбрать ровно 6 вершин. Тогда каждого цвета выбрано по 2 вершины. Либо выбранные и невыбранные вершины чередуются (тогда образовывается много треугольников), либо какие-то 2 выбранные вершины идут подряд. Рассмотрим их (рисунок 2). Вершины левее и правее выбирать нельзя, т.к. образуется треугольник. Но эти 2 вершины были одного цвета. Осталось только 2 другие вершины этого цвета. Мы должны выбрать их (рисунок 3). Можно отметить вершины, которые нельзя выбирать, красным (это делается перебором - для каждой вершины смотрим, образуется ли треугольник, если ее выбрать). Рисунок 4. Остается 2 точки. Мы обязаны их выбрать (чтобы всего было 6). Но тогда все равно образуется треугольник (например, из 3 подряд идущих точек). Противоречие.
Значит, больше 5 вершин выбрать нельзя. Пример на 5: Рисунок 5 (по-моему, он верный).

Пошаговое объяснение:
1. 1) (-7/2)^0=1 - любое отличное от нуля выражение в степени 0 равно 1
2) 3.8^0-3.4^0=1-1=0
3) 5^3*1/5^3=1 - тк нужно сократить выражение на 5^3
3. 1) 1/2^0+1/2^1+1/2^2+1/2^3
вычислите степень
1/1+1/2+1/4+1/8
1/1 - это и есть 1
1+1/2+1/4+1/8
8+4+2+1/8=15/8
ответ:15/8
2)(1/10)^0+(1/10)^1+(1/10)^2+(1/10)^3
1+1/10+1/100+1/1000
вычислим сумму
1000+100+10+1/1000=1111/1000
ответ: 1111/1000
3)(5/6)^2*9/10:5/8:(11/4)^0
25/36*9/10:5/8
25/36*9/10*8/5
25/4*1/10*8/5
5/4*1/10* 8
5/4*1/5*4
1/4*4=1
ответ:1