
Здесь важно сделать оговорку, что задача имеет смысл без чертежа только если порядок следования букв в названии треугольников важен. (см. рисунок)
Тогда из того, что ΔABС = ΔBAD следует, что ∠BAC = ∠ABD (∠A ΔABC соответствует ∠B ΔBAD). Они - накрест-лежащие, AB - секущая ⇒ CB ║ AB (признак параллельности прямых)
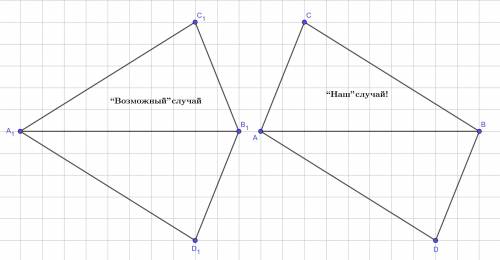
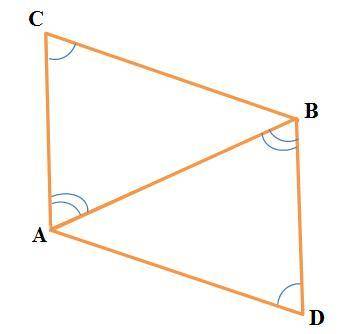
По условию треугольники ABC и BAD равны. Тогда:
1) сторона АВ и BA совпадают и AC=BD, BC=AD (см. рисунок);
2) ∠C=∠D, ∠ABC=∠BAD, ∠BAC=∠ABD.
Признак параллельности прямых: Если при пересечении секущей двух прямых накрест лежащие углы равны, то эти прямые параллельны.
Так как накрест лежащие углы ∠BAC и ∠ABD равны, то прямые, проходящие через стороны AC и BD параллельны. Отсюда, стороны AC и BD параллельны.
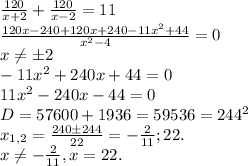
Рассмотрим выражение вида 7 - 2 * × = 9 * × - 8 * (× + 1). Для того чтобы найти значения переменной x, надо слагаемые с переменной x перенести в левую часть и сменить
знаки у слагаемых при переносе и слагаемые без переменной x перенести в правую часть и сменить знаки на противоположные при переносе. Затем, выразим переменную x
и найдем корень (корни) уравнения.
Рассмотрим 7 - 2 * × = 9 * × - 8 * (× + 1). Выразим переменную x и найдем корень уравнения.
7 - 2 * × = 9 * × - 8 * (× + 1)
7 - 2 * x = 9 * x - 8 * x - 8
7 - 2 * x = x - 8
-2 * x - x = -8 - 7
-3 * x = -15
x = (-15) : (-3)
x = 5.
Получили, что уравнение имеет 1 корень x = 5.
ответ: при значении x = 5 выражение 7 - 2 * x и 9 * x - 8 * (x + 1) принимают равные значения