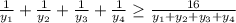10 500 г. до н.э. в Ирландии был построен Стоун Хендж.
По преданию каменный Стоун Хендж был построен в Ирландии великанами. Они расположили их по кругу («круг великанов»). См. Баальбек. Ливан. Гёбекли-Тепе. Турция. Саксайуаман.Ю.Америка.
Древние греки считали, что их сооружали одноглазые гиганты-циклопы. Считалось, что эти камни могли передвигаться самостоятельно с волшебного слова» или под музыку Орфея.
"Британские острова были населены Расой гигантов до появления там первых людей". В Лондоне возвышалось огромное гранитное изваяние Ога - короля Огама - и статуя его жены, королевы Магог; во время второй мировой войны эти статуи погибли в бомбежке.
Для начала докажем то, что называется неравенством Коши-Буняковского-Шварца:
Рассмотрим два набора чисел: 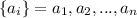 и
и 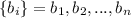 .
.
Тогда выполнено неравенство: 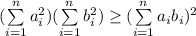 ;
;
Это неравенство можно доказывать по-разному. Заметим, что скалярное произведение векторов 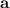 и
и 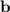 есть
есть 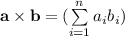 , где
, где 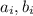 - координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как
- координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как 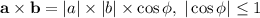 ), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).
), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).
__________________________
Сделаем замену: 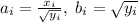 ; Получим неравенство:
; Получим неравенство: 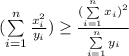
Полагая 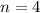 и
и 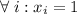 , получим:
, получим: