На рисунке во вложении: ВС = 13, АД = 28.
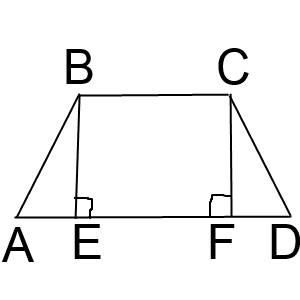
1) проведем высоты трапеции ВE и CF, как показано на рисунке во вложении.
2) фигура ВСFE - прямоугольник, а в прямоугольнике противоположные стороны равны. Значит BC = EF = 13 см.
3) Рассмотрим прямоугольные треугольники АВЕ и CFD, они равны по гипотенузе и острому углу (АВ=СД по условию "трапеция равнобедренная", а углы при основании равнобедренной трапеции равны, следовательно угол BAE = CDF).
4) Из равенства треугольников следует, что АЕ = FD.
5) Т.к. AD = 28 см, а EF= 13 см, то AD-EF=AE+FD=28-13=15 см. Тогда если АЕ=FD, то AE=15/2 = 7,5 см.
6) рассмотрим треугольник АВЕ, в нем угол А=60 градусов, Е = 90, на угол В остается 30 градусов.
7) по теореме "В прямоугольном треугольнике сторона, напротив угла 30 градусов, в два раза меньше гипотенузы" следует, что гипотенуза АВ= 2*7,5 = 15 см.
8) СД=АВ=15 см.
9) Периметр равен АВ+ВС+СД+ДА = 15 + 13 + 15 + 28 = 71 см.
ответ: 71 см.
ок! принимаем расстояние от А до В за 1 - единицу.
тогда скорость катера из пункта А в пункт В - 1/4,
скорость плота - 1/40.
скорость плота - это у нас и будет скорость течения.
Скорость плота из А в В будет состоять из скорости катера и еще скорости течения. Вычитаем из скорости катера скорость течения:
1/4-1/40=9/40 - это собственная скорость катера.
чтобы найти скорость катера из В в А, нужно из скорости катера еще раз вычесть скорость течения:
9/40-1/40=8/40=1/5 - скорость катера против течения из В в А.
Теперь находим время, за которое катер доплывет из В в А:
путь делим на скорость, то есть делим 1/(1/5)=5 часов.
ответ: 5 часов.
2 лодка-15
х+9=15+12
х=15+12-9
х=18, было в 1 лодке.