720
Пошаговое объяснение:
Сначала вычеркнем из набора чисел 1, 2, ..., 1000 числа, кратные 7; их количество равно 1000/7 = 142. Затем из того же набора чисел 1, 2, ..., 1000 вычеркнем числа, кратные 11; их количество равно 1000/7 = 90 и так же с 13 - 1000/13 = 76(берем только целую часть числа).
Стоит учесть, что при таком мы вычеркнем числа кратные 77(7*11), 143 (11*13) и 91(7*13) дважды. количество таких цифр будет:
1000 / 77 = 12
1000 / 91 = 10
1000 / 143 = 6
Значит, всего мы вычеркнули 142 + 90 + 76 – 12 - 10 - 6 = 280 чисел, а осталось 1000 – 280 = 720 чисел.
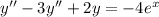
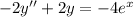
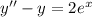
Общее решение неоднородного дифференциального уравнения представляет собой сумму общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
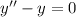
Составим характеристическое уравнение:
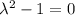
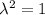
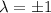
Тогда, частное решение запишется в виде:
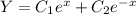
Частное решение данного неоднородного уравнения ищем в виде:
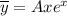
Находим вторую производную:
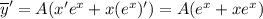
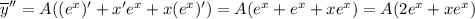
Подставляем в уравнение:
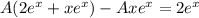
Разделим уравнение на экспоненту:
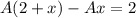
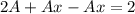
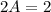
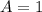
То есть частное решение имеет вид:
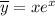
Записываем общее решение исходного уравнения:
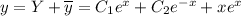
ответ: 6
Удачи!