Для наглядности удобно провести некоторое соответствие с трехмерным пространством
Понятно что z(x,y) можно в нем изобразить как некоторую поверхность
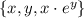
Точке (1,4) соответствует 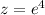 , т.е. точка
, т.е. точка 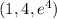 (*)
(*)
Линию 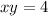 удобнее записать как трехмерную кривую
удобнее записать как трехмерную кривую 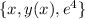 , что будет пересекать поверхность z(x,y) при x=1
, что будет пересекать поверхность z(x,y) при x=1
Запишем уравнение касательной к этой кривой в точке 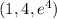 , в качестве параметра берем переменную x
, в качестве параметра берем переменную x
 (#)
(#)
(вычисляется по аналогии с 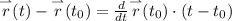 )
)
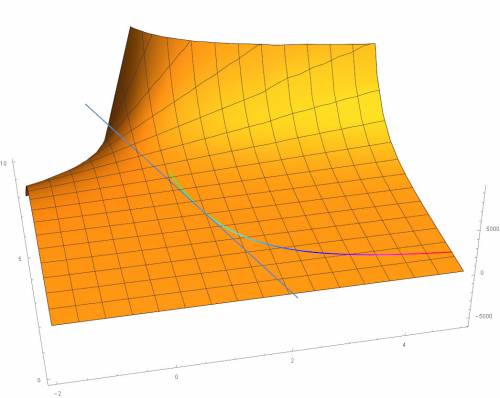
В прикрепленном файле нарисована поверхность, кривая и касательная.
Зная уравнение касательной, построим единичный вектор в направлении убывания x:
Пусть x=0, тогда из (#) получим точку 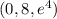
Соотв. единичный вектор в направлении этой точки из (*) имеет вид
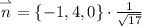
Понятно что z компонента никак не повлияет на значение производной по направлению, формально вектор можно записать как
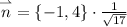
И, наконец, найдем искомую производную:
![grad[z(M_0)]\cdot\overset{\rightharpoonup }{n}=\left\{e^4,1 \cdot e^4\right\} \cdot \{-1,4\}\cdot\frac{1}{\sqrt{17} } = \frac{3 e^4}{\sqrt{17}} \approx 39.726](/tpl/images/0992/5590/2e9d7.png)
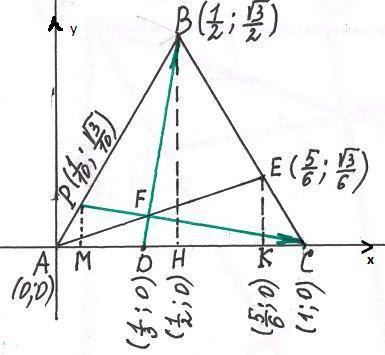
В равностороннем треугольнике ABC на сторонах AC и BC отметили точки D и E такие, что CD=2AD, BE=2CE. Обозначим точку пересечения отрезков AE и BD через F. Чему равен угол BFC?
Пошаговое объяснение:
1) Введем прямоугольную систему координат .Пусть АВ=ВС=АС=1. Пусть FC∩АВ=Р .Пусть ЕК⊥АС, ВН⊥АС, РМ⊥АС.
2) Определим координаты точек .
А(0;0) ,В(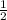 ;
;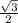 ) ,С(1;0) ,Н(0,5 ;0) ,D(
) ,С(1;0) ,Н(0,5 ;0) ,D( 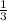 ;0) ,К(
;0) ,К( 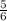 ;0) , Е(
;0) , Е(
3)Найдем координаты направляющих векторов: DB( 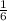 ;
;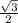 ) , РС(
) , РС( 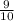 ;
;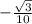 ).
).
4)Найдем скалярное произведение векторов .
DB *РС= 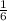 *
* 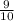 +
+ 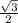 *(
*(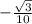 ) =
) =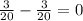 ⇒вектор DB⊥PC ⇒∠BFC=90°.
⇒вектор DB⊥PC ⇒∠BFC=90°.
=======================================
Пояснения( жуткие вычисления , слабонервным можно не читать).
1) Координаты точки Е. ΔКСЕ прямоугольный .
КЕ=СЕ*sin60= 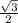 *
* 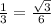 .
.
КС=СЕ*cos60= 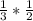 =
=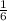 , поэтому АК= 1-
, поэтому АК= 1-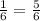 → Е(
→ Е( 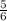 ;
;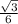 ) .
) .
2)Координаты точки В. ΔАВН- прямоугольный .
АН=НС= 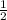 .
.
ВН=АВ*sin60=1* 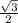 =
=
3)Ищем координаты точки Р
а)ΔВDC , по т. Менелая 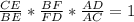 ,
, 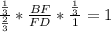 ,
, 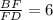 .
.
б)ΔАВD , по т. Менелая 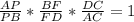 ,
, 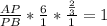 ,
, 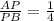 ,
,
AP=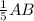 =
= 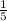 .
.
в)ΔАРМ прямоугольный .
РМ=АР*sin60=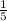 *
* 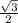 =
= 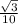 .
.
АМ=АР*cos60= 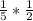 =
=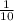 → P (
→ P ( 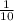 ;
;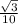 ) .
) .
1)29350+8350=37700-72=37628
2)37628*7=263396:92=2863
3)2863+28911=31774
4)81:9=9*24=216
5)31774-216=31558