– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ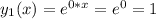
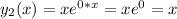
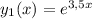
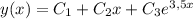
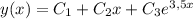
– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ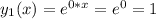
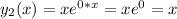
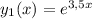
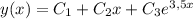
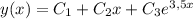
b2=b1*q
b3=b1*q^2
b4=b1*q^3
b1*+b1*q+b1*q^2+b1*q^3=15
b1*(1+q+q^2+q^3)=15 1+q+q^2+q^3=15/b1 (1 уравнение)
(1/b1)+(1/b1*q)+(1/b1*q^2)+(1/b1*q^3)=1,875
Приведём к общему знаменателю.
(q^3+q^2+q+1)/b1*q^3=1,875
q^3+q^2+q+1=1,875*b1*q^3 подставим 1 уравнение
15/b1=1,875*b1*q^3
b1^2*q^3=8, так как все числа натуральные, то b1=1 q=2
b2=1*2=2
b3=1*2^2=4
b4=1*2^3=8
1+2+4+8=15
1+(1/2)+(1/4)+(1/8)=1+0,5+0,25+0,125=1,875