Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида) . Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
Пошаговое объяснение:
а) Пестрик; b) Черныш; с) Пестрик; d) Пестрик
Пошаговое объяснение:
Исходя из этих данных, можно составить в каждом случае уравнение и по нему определить кто взял последним.
Формула нашего уравнения будет следующая:
х=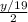
y - Это количество початков.
первым по порядку у нас идет Пестрик, если он взял последние 19 початков число будет с дробью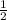 
и больше, если число будет цельным, либо с другой дробью которая меньше 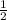, значит последние 19 початков за Чернышом.
а) х=(323/19)/2
х=17/2
х=8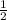 (Пестрик)
б) х=(621/19)/2
х=621/38
х=16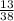
(Черныш)
с) х=(455/19)/2
х=455/38
х=11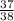
(Пестрик)
d) х=(400/19)/2
х=400/38
х=10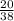
(Пестрик)
Решение во вложении :)
И если не трудно выберите за лучший ответ :)
#Azerbaijan
#CleverAlex