а) (х+1)²>0 х∈(-∞;-1)∪(-1;+∞), т.к. при х=-1 левая часть обращается в нуль. но нуль не может быть больше нуля. ответ объединение двух промежутков.
б) 4х²-х+9<0 дискриминант левой части равен 1-4*36<0 a=4>0, значит, для любого действительного х левая часть неравенства больше нуля. нулю она тоже не равна. т.к. дискриминант меньше нуля. а это означает. что неравенство не имеет решений.
с) -х²+4х-7=0, дискриминант 16-28 отрицательный. значит. парабола не пересекается с осью ох, находится ниже оси. т.к. первый коэффициент равен минус один, ветви направлены вниз, значит, для любого х левая часть меньше, а не больше нуля. т.е. неравенство решений не имеет.
д) (х-3)(х+3)<0 решим методом интервалов. корни левой части ±3
___-33
+ - +
х∈(-3;3)
Задание 1.
во вложениях
Задание 2.
Пусть 3х - яблонь в саду, тогда х - груш.
По условию задачи, когда вырубили 14 яблонь и посадили 10 груш, деревьев стало поровну.
Составим и решим уравнение:
3х - 14 = х + 10
3х - х = 10 + 14
2х = 24
х = 12 - количество груш в саду
Т. к. по условию задачи яблонь в 3 раза больше, чем груш, то:
12 × 3 = 36 - количество яблонь в саду
ответ: 12 груш и 36 яблонь.
Задание 3.
а) 3( х + 0,6) = 3 - х
3х + 1,8 = 3 - х
3х + х = 3 - 1,8
4х = 1,2
х = 0,3
ответ: 0,3.
б) во вложениях
Задание 4.
2,5 : 8,75 = х : 21
х = 2,5 × 21 ÷ 8,75
х = 6
ответ: 6.
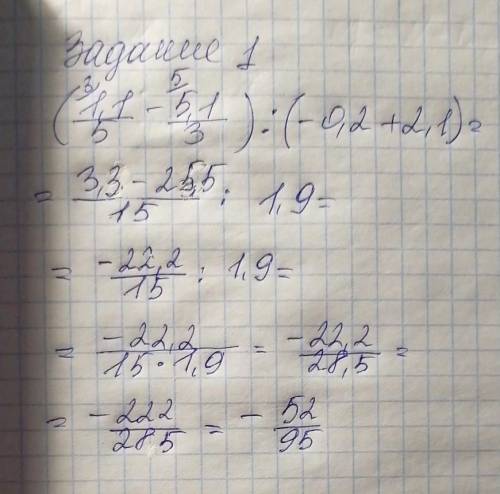

2000*1,15 = 2300 (тг) - новая цена
27600 : 2300 = 12 (билетов)
ответ: 12 билетов