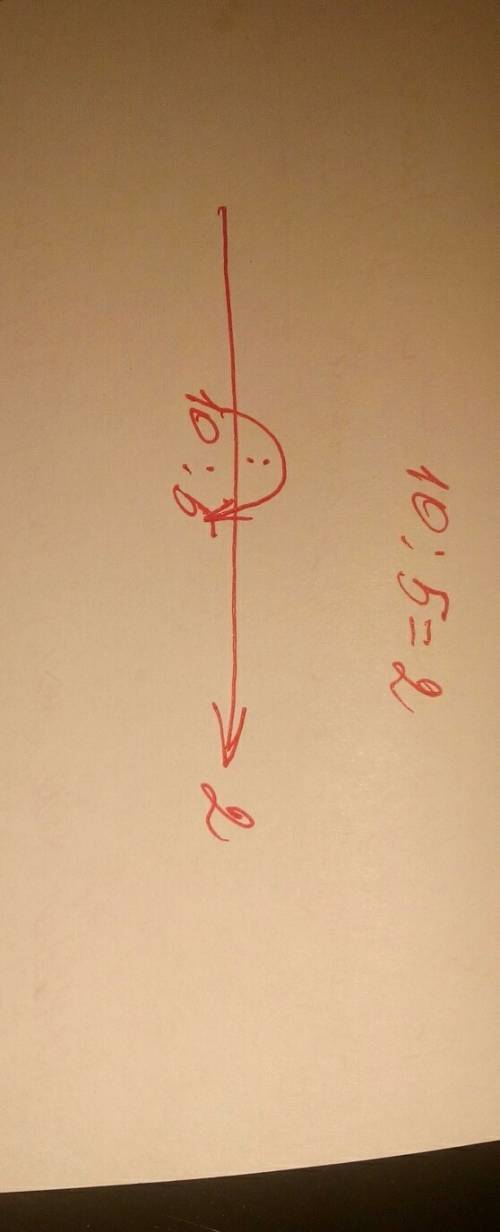
сумма n последовательных нечетных натуральных чисел при n>1
1+3+5+7+...+(2n-1)=n^2
Доказательство методом математической индукции
База индукции
n=2. 1+3=2^2
Гипотеза индукции
Пусть для n=k утверждение выполняется, т.е. выполняется
1+3+5+7+...+(2k-1)=k^2
Индукционный переход. Докажем, что тогда выполняется утверждение и для n=k+1, т.е, что выполняется
1+3+5+7+...+(2k-1)+(2K+1)=(k+1)^2
1+3+5+7+...+(2k-1)+(2K+1)=используем гипотезу МИ=k^2+(2k+1)=k^2+2k+1=используем формлу квадрату двучлена=(k+1)^2, что и требовалось доказать.
По методому математической индукции формула справедлива.
Число n^2 при n>1 zвляется составным, оно делится на 1,n,n^2.
А значит сумма n последовательных нечетных натуральных чисел при n>1 является составным числом. Доказано
На рисунку зобразимо коробку у перерізі у трьох різних ракурсах (рис 5.1.1). Позначимо сторони коробки a =5 см = 0,05 м, b = 8 см = 0,08 м, c=18 см=0,18 м, товщина стінок h=1,5 см=0,015 м. З рисунків слідує, що порожнина коробки теж має форму прямокутного паралелепіпеда зі сторонами (a‒2h), (b‒2h), (с‒2h).
рис. 5.1.1
ІІ. Записуємо скорочену умову задачі та її розв’язок.
Дано:
а=0,05 м
b=0,08 м
с=0,18 м
h=0,015 м
ρС=11 000 кг/м3
g=10 Н/кг
F - ?
Сила земного тяжіння, яка діє на коробку прикладена до центра мас коробки та направлена до центру Землі (вертикально вниз) (рис 5.1.2)
рис. 5.1.2
Силу тяжіння можна знайти за формулою:
F=mg (1) де m - маса коробки.
Оскільки маса повітряної порожнини всередині коробки значно менша маси стінок (оскільки густина повітря набагато менша за густину свинцю), вважатимемо, що маса коробки m - це маса лише свинцевих стінок. Масу стінок знайдемо з формули густини:
звідки (2)
де VС - об’єм стінок коробки. Цей об’єм знайдемо віднявши від об’єму усієї коробки V та об’єму порожнини VП:
VС =V‒ Vп (3)
З рис 5.1 слідує, що об’єм коробки: (4)
об’єм порожнини: (5)
підставимо (4) та (5) в (3): (6)
підставимо (6) в (2): (7)
підставимо (7) в (1): (*)
Виконаємо перевірку розмірності:
Виконаємо обчислення:
Відповідь: F= 62,7 Н