Задача. Подбрасывается 12-гранный кубик, на гранях которого написаны числа от 1 до 12. Вероятность выпадения i-ой грани пропорциональна (с одним и тем же коэффициентом пропорциональности) числу, написанному на этой грани, то есть,
P(выпало число i) = k * i
Вероятность выпадения k,2k,3k,...,12k. Сумма вероятностей k + 2k + 3k + ... +12k = 78к должна равняться 1, т.е. 78k = 1 откуда k = 1/78
Число очков большее чем 6 это 7, 8, 9, 10, 11, 12.
Вероятность того, что выпало число очков, большее 6, равна
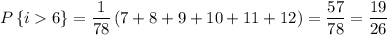
ответ: k = 1/78 и P = 19/26
4cos^2x+sinx-1=0
4(1-sin^2x)+sinx-1=0
4-4sin^2x+sinx-1=0
-4sin^2x+sinx+3=0
Пусть sinx=t ; |t|<=1
-4t^2+t+3=0
D=1+48=49 √D=√49=7
t1=-1+7/-8=-3/4
t2=-1-8/-8=1
sinx=-3/4 sinx=1
x=(-1)^n-1arcsin3/4+n, n прин. Z x=/2+n, n прин. Z
ответ: (-1)^n-1arcsin3/4+n; /2+n
sin^2x-6sinx*cosx+5cos^2x=0|:cos^2x
tg^2x-6tgx+5=0
Пусть tgx=t
t^2-6t+5=0
D=36-20=16 √D=√16=4
t1=6+4/2=5
t2=6-4/2=1
tgx=5 tgx=1
x=arctg5+k, k прин. Z x=/4+k, k прин. Z
ответ: arctg5+k; /4+k