Один покупатель заплатил 480 рублей за 3 метра ткани, а второй купил такой же ткани на 800 рублей. сколько - id764240220210125 от chernecov1977 25.01.2021 20:19

Question

Математика: Один покупатель заплатил 480 рублей за 3 метра ткани, а второй купил такой же ткани на 800 рублей. сколько метров ткани купил второй покупатель?

chernecov1977 · Accepted Answer

Сначала сократить как обычную дробь. Тут получиться три пары чисел, которые можно сократить: 1,7 и 5,1; 4,92 и 0,82; 7,2 и 4,8. Сокращать можно, если оба числа возможно поделить на одну и ту же цифру (например 1,7 и 5,1 можно поделить на 1,7, то есть получится 1 и 3 соответственно. Теперь, в дроби, вместо 1,7 будет стоять 1, а вместо 5,1 будет 3)

Сокращаем и получаем:

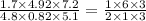
$\frac{1.7 \times 4.92 \times 7.2}{4.8 \times 0.82 \times 5.1} = \frac{1 \times 6 \times 3}{2 \times 1 \times 3}$

Дальше все числа в числителе и знаменателе перемножаем, чтобы получить только одно число сверху, и только одно снизу:

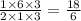
$\frac{1 \times 6 \times 3}{2 \times 1 \times 3} = \frac{18}{6}$

Из получившейся дроби пробуем вынести целое число:

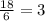
$\frac{18}{6} = 3$

Всё, пример решён, ответ 3

Один покупатель заплатил 480 рублей за 3 метра ткани, а второй купил такой же ткани на 800 рублей. сколько метров ткани купил второй покупатель?

MOGZ ответил