Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
ответ: – 8.
Пример 3. Решите уравнение .
. Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
ответ: 3.
Пример 4. Решите систему
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
ответ: (1; 1).
Замечание. Если неизвестные системы х и у, то ответ можно записать в виде ко
Пошаговое объяснение:
надеюсь правильно
Пошаговое объяснение:
ДАНО: Y = x³/(x-1)
Исследование
1. Область определения: D(х)= R\{1} = (-∞;1)∪(1;+∞).
Не допускаем деления на 0 в знаменателе.
2.Поведение в точке разрыва. LimY(1-)= -∞, LimY(1+)= +∞. Вертикальная асимптота - х = 1. Неустранимый разрыв II-го рода.
3. Поведение на бесконечности - наклонная асимптота.
k = lim(+∞)Y(х)/x = х³/(x²+ x) = ∞ - коэффициент наклона.
Наклонной асимптоты нет.
4. Нули функции, пересечение с осью ОХ. Y(x) = 0.
5. Пересечение с осью ОУ. Y(0) = 0
6. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(0;1).
Положительна: Y>0 - X∈(-∞;0)∪(1;+∞)
7. Проверка на чётность.
Функция со сдвигом от осей симметрии - функция общего вида.
Ни нечётная: Y(-x) ≠ -Y(x) ни чётная: Y(-x) ≠ Y(x)
8. Поиск экстремумов по первой производной.
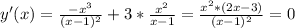
Корни квадратного уравнения. х1 = 0 и х2= 3/2 = 1,5.
9. Локальные экстремумы.
Минимум: Y(1,5) = 6.75 , Максимум: Y(0) = 0
10. Интервалы монотонности.
Возрастает: X∈(1.5;+∞)
Убывает: Х∈(-∞;1)∪(1;1.5)
11. Поиск перегибов по второй производной.
y''(x) = 2*x*(x²-3*x+3)/(x-1)² = 0
x = 0 и точка разрыва при Х = 1.
12. Выпуклая - 'горка' - X∈(0;1).
Вогнутая - 'ложка'- X∈(-∞;0)∪(1;+∞;).
13. Область значений. E(y) - y∈(-∞;+∞).
Рисунок с графиком функции в приложении.

2)3/4