Вдвух бочках 88 л бензина. если из первой бочки перелить во вторую 10 л бензина, то во второй бочке - id765045720230407 от aminochka1516 07.04.2023 06:17

Question

Математика: Вдвух бочках 88 л бензина. если из первой бочки перелить во вторую 10 л бензина, то во второй бочке окажется на 20% бензина больше, чем в первой. сколько литров бензина в каждой бочке?

aminochka1516 · Accepted Answer

1. Область определения x ∈(-∞,+∞), функция - чётная

2. y' = -x³+2x

3. y'=0, 2x-x³=0, x(2-x²)=0, стационарные точки x=0, x=± $\sqrt{2}$

4. y'>0, x>0, x< $\sqrt{2}$ , x∈(0,

y'>0, x<0, x< - $\sqrt{2}$ , x∈(-∞,-

Тогда промежуток возрастания x ∈(-∞,- $\sqrt{2}$ )∪(0,

Промежуток убывания x ∈ (- $\sqrt{2}$ ,0)∪(

В точке x = 0, производная меняет знак с минуса на плюс, то есть x=0 - точка минимума

в окрестности точек x=± $\sqrt{2}$ производная меняет знак с плюса на минус, это точки максимума

y(0)=0

y(± $\sqrt{2}$ )=2-1=1

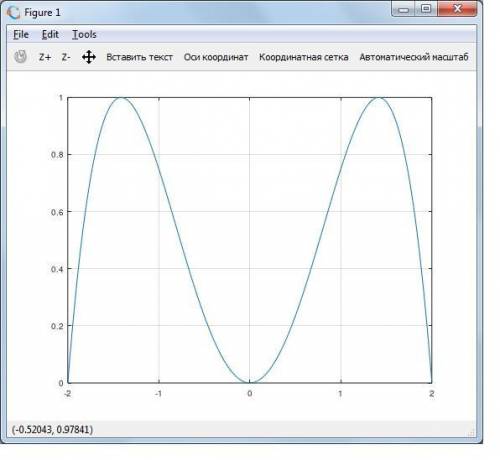
вот и график, построенный в Октаве

Пошаговое объяснение:

У = - ¼ ∙ х^4 + х^2 Найти: 1. область определения функции; 2. производную функции; 3. стационарные т

MOGZ ответил