В) 5 минут
Пошаговое объяснение:
Дано:
V катера - 1 км за 2 мин = 500 м/мин
V лодки - в 5 раз больше T катера
Расстояние между ними - 3 км = 3 000 м
Найти:
Через сколько они встретятся - ? мин
1) 1 · 5 = 5 (мин) - Столько времени тратит лодка на 500 м.
2) 500 : 5 = 100 (м/мин) - V лодки
3) 100 + 500 = 600 (м/мин) - V сближения
T = S : V (T - время, S - расстояние, V - скорость
4) 3 000 : 600 = 5 (мин) - T через которое они встретятся
Теперь посмотрим варианты ответов:
А) 2 мин
Б) 3 мин
В) 5 мин
Г) 6 мин
В) 5 минут
Формула, устанавливающая зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то S₁ = 7,2 (см²)
2) если h = 2, то S₂ = 7,2h = 14,4 (см²)
1) если h = 3,6, то S₃ = 7,2h = 25,92 (см²)
Пошаговое объяснение:
Требуется записать формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h. Пользуясь формулой, вычисли S, если h = 1; 2; 3,6.
Площадь боковой поверхности параллелепипеда найдем по формуле:
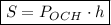 , где Р - периметр основания, h - высота.
, где Р - периметр основания, h - высота.
По условию Росн. = 7,2 см.
Составим формулу, устанавливающую зависимость площади боковой поверхности параллелепипеда S от длины его высоты h:
S = 7,2h
1) если h = 1, то
S₁ = 7,2h = 7,2 · 1 = 7,2 (см²)
2) если h = 2, то
S₂ = 7,2h = 7,2 · 2 = 14,4 (см²)
1) если h = 3,6, то
S₃ = 7,2h = 7,2 · 3,6 = 25,92 (см²)
1) Площадь большого квадрата S = 36 см²
Очевидно, что маленький квадрат может иметь сторону только 1 см,
так как 10 квадратов со стороной 2 см дадут общую площадь 40 см²
Таким образом, 10 квадратов по 1 см² каждый дадут 10 см² общей
площади.На 2 прямоугольника остается:
2S₂ = S - 10S₁ = 36 - 10 = 26 (см²)
S₂ = 26:2 = 13 (см²)
2) Площадь малого квадрата S₁ = 36 см².
Общая площадь, занимаемая квадратами: 10S₁ = 10*36 = 360 (см²)
Расположение малых квадратов в большом может быть только в двух
вариантах: или 10*1 или 5*2.
При любом другом расположении в оставшейся части большого
квадрата невозможно будет разместить два равных прямоугольника.
а) расположение 10*1. Большой квадрат в этом случае будет иметь
сторону, равную:
b = 10√S₁ = 10*6 = 60 (см)
Площадь, оставшаяся для прямоугольников:
2S₂ = b² - 10S₁ = 3600 - 360 = 3240 (см²)
S₂ = 3240:2 = 1620 (см²)
b) расположение 5*2. Большой квадрат в этом случае будет иметь
сторону, равную:
b = 5√S₁ = 5*6 = 30 (см)
Площадь, оставшаяся для прямоугольников:
2S₂ = b² - 10S₁ = 900 - 360 = 540 (см²)
S₂ = 540:2 = 270 (см²)