
Пошаговое объяснение:
Заметим, что если x - корень уравнения, то (-x) - тоже корень. Чтобы корней получилось нечетное число, один из корней должен быть нулем. Подставляем x = 0:
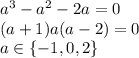
Проверяем, удовлетворяют ли условию найденные a. Для этого достаточно проверить, что при подстановке найденных a уравнение имеет ровно один положительный корень.
1) a = -1:
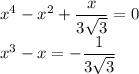
Рассмотрим функцию 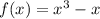 . Её производная
. Её производная 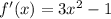 принимает неотрицательные значения при
принимает неотрицательные значения при  и неположительные значения при
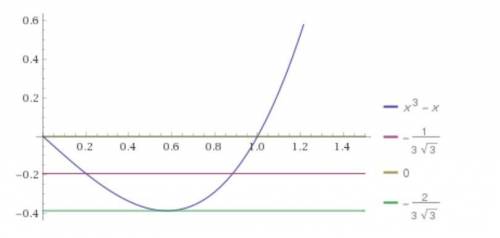
и неположительные значения при 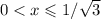 . Значит, график функции f(x) при x > 0 выглядит примерно так, как изображено на рисунке: при x, близких к 0, значение близко к 0, затем убывание, в точке
. Значит, график функции f(x) при x > 0 выглядит примерно так, как изображено на рисунке: при x, близких к 0, значение близко к 0, затем убывание, в точке 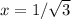 принимается минимальное значение
принимается минимальное значение  , потом неограниченное возрастание.
, потом неограниченное возрастание.

Значит, у уравнения 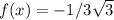 есть два положительных корня, не подходит.
есть два положительных корня, не подходит.
2) a = 0: аналогично, можно свести к уравнению f(x) = 0, у него один положительный корень x = 1. Подходит!
3) a = 2: аналогично, сводится к уравнению 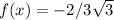 . У этого уравнения тоже только один положительный корень
. У этого уравнения тоже только один положительный корень 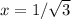 .
.
42• 1/2-15/6+2/3
21-15,6+2/3
5,4+2/3
54/10+2/3
27/5+2/3
81+10/15
91/15