Находим абсциссы точек пересечения прямых с осью Ох.
x-2y+4=0, y=0, х = -4.
y=2x+3, y=0, х = -3/2 = -1,5.
Теперь определяем точку пересечения прямых.
Первую прямую выразим относительно у =(1/2)х + 2
(1/2)х+2=2x+3,
1,5х = -1,
х = -2/3.
Теперь можно переходить к площади.
Заданная фигура состоит из двух частей.
Первая S1 - ограничена прямой у = (1/2)х + 2, осью Ох и двумя прямыми х = -4, х = -1,5.
Вторая S2- заключена между наклонными прямыми и прямыми х = 1,5 и х = -2/3.
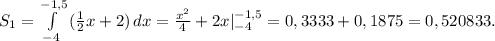
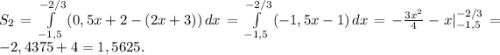
Получаем ответ: S = 0,520833+1,5625 = 2,083333 = 25/12.
этот результат легко проверить:
S = (1/2)*2.5*(5/3) = 25/12.
Здесь (5/3) - ордината точки пересечения прямых.
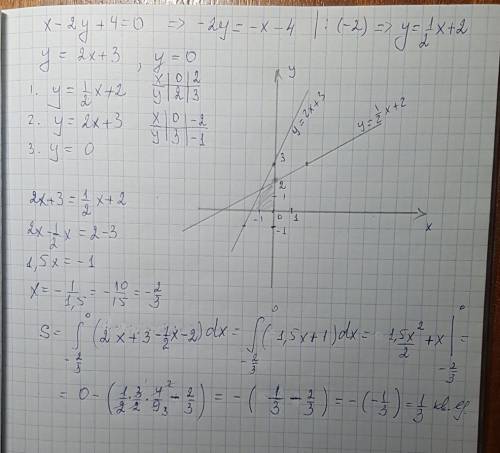
Находим абсциссы точек пересечения прямых с осью Ох.
x-2y+4=0, y=0, х = -4.
y=2x+3, y=0, х = -3/2 = -1,5.
Теперь определяем точку пересечения прямых.
Первую прямую выразим относительно у =(1/2)х + 2
(1/2)х+2=2x+3,
1,5х = -1,
х = -2/3.
Теперь можно переходить к площади.
Заданная фигура состоит из двух частей.
Первая S1 - ограничена прямой у = (1/2)х + 2, осью Ох и двумя прямыми х = -4, х = -1,5.
Вторая S2- заключена между наклонными прямыми и прямыми х = 1,5 и х = -2/3.
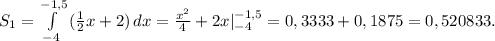
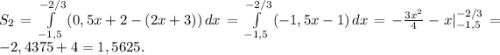
Получаем ответ: S = 0,520833+1,5625 = 2,083333 = 25/12.
этот результат легко проверить:
S = (1/2)*2.5*(5/3) = 25/12.
Здесь (5/3) - ордината точки пересечения прямых.

1) X + Y + Z = 56
2) Y = 1/2*X
3) Z = X - 4
Решаем методом подстановки
4) X + X/2 + X-4 = 56
Упрощаем
5) 2 1/2 *Х = 56 + 4 = 60
Находим неизвестное - Х.
6) X = 60 : 2 1/2 = 24 - ОТВЕТ
Находим неизвестное - Y
7) Y = X/2 = 2422 = 12 - ОТВЕТ
Находим неизвестное - Z
8) Z = X -4 = 24 - 4 = 20 - ОТВЕТ
ИЛИ в одно выражение, если дополнить словами, если Х, то Y= X/2 и Z=X-4
1) X+ X/2 + (X-4) = 56
Далее решаем как и после уравнения 4).