1) зачеркнули 7 из числа 17;
2) зачеркнули 8 из числа 85.
Решение 1:Искомое двузначное число представим в виде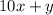 
(
и 
- однозначные и неотрицательные, при этом 
).
1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа 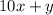получилось число . Нам нужно выполнение следующего равенства:
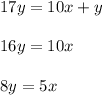
Единственные однозначные натуральные решения: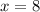 
и 
.
Значит, число 
⇒ 
.
2). Пусть зачеркнули цифру из разряда единиц. 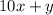⇒ . Уравнение составляется и решается по аналогии:
Откуда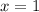 
и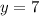 
.
Имеем второе подходящее решение: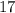 
⇒ 
.
Значит, двузначное число - это 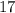или , или .
Можно было и кратким подбором решить, умножая все цифры на 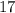(умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
- не подходит, не двузначное.
- подходит, вычеркивали 
из числа .
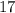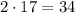- не подходит.
- не подходит.
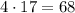- не подходит.
- подходит, вычеркивали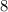 
из числа .
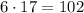- не подходит, начинаются трехзначные числа.
Получаем те же самые два решения: 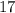и .
Рисунок во вложении.
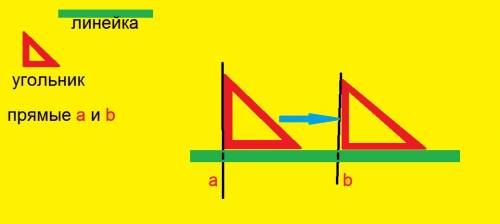
1. Нарисовать две прямые а и b.
2. Совместить сторону (катет) прямого угла угольника с прямой а, а к другой стороне (катету) приложить линейку.
3. Двигать угольник по линейке до прямой b.
4. Проверить, если та сторона, которая была совмещена с прямой а, совмещается, также, и с прямой b.
Если совмещается, то прямые параллельны, если нет - то не параллельны.
На рисунке видно, что сторона угольника не совместилась с прямой b, значит эти прямые не параллельны.
ответ: построение параллельных прямых неточное, a ∦ b.
При данной проверке подтвеждается правило параллельности прямых: " Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны."
В роли третьей прямой выступает линейка, а угольник проверяет, если углы пересечения прямых а и b с линейкой равны.
