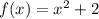 определена на множестве E
определена на множестве E 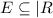
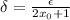 где
где 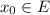 .
. на области
на области 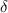 от
от  (то есть:
(то есть: 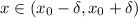 ) выполняется
) выполняется 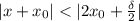 .
.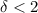 , выполняется
, выполняется 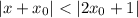 .
.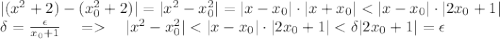
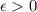 есть
есть 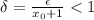 , на области которой выполняется
, на области которой выполняется 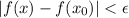
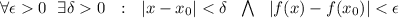 ). Следовательно -
). Следовательно - 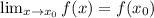 .
.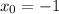 нужно отдельно доказать предел
нужно отдельно доказать предел 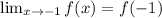 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 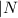 тоже подмножество
тоже подмножество  , значит
, значит 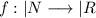 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 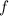 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 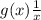 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 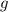 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 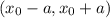 "...
"...1 полоса может быть любой из 3х цветов,
2 полоса уже любой из 2х (т.к. первая уже заняла какой-то цвет),
3 полосе остается только 1 цвет
3*2*1=6
Пошаговое объяснение:
1) 4 варианта (мартышка, осёл, козел, мишка)
2) 3 варианта (на первом месте уже кто-то есть)
3) 2 варианта
4) 1
4*3*2*1=24
1) 25 вариантов (любой человек из класса)
2) 24 варианта (все, кром выбранного старосты)
25*24=600
1) 4 варианта (кроме математики)
2) 3 варианта
3) 2 варианта
4) 1 вариант
5) 1 вариант (математика)
4*3*2*1*1=24
5. 12 вариантов
1)1 рубашка: 2брюк*2обуви=4 варианта
2)4*3рубашки=12
6. 6 видов
1)батон: 3 варианта
2)черный хлеб: 3 варианта
5+4 =9 фруктов
9*1=9 вариантов
9. 8 фотографий
8*1=8