1. Натуральные числа, противоположные им числа и число 0 составляют множество целых чисел. Z = {... -3, -2, -1, 0, 1, 2, 3 ...}.
2. Натуральное число и отрицательное число, полученное из натурального приписыванием к нему знака минус (-), называют противоположными числами.
3. Из двух целых чисел больше то, которое в ряду целых чисел стоит правее, и меньше то, которое стоит левее.
4. Сумма двух положительных чисел положительная (+), а сумма двух отрицательных чисел отрицательная (-).
5. Сумма противоположных чисел равна 0.
6. Сумма двух чисел разных знаков может быть как положительной, так и отрицательной. Знак суммы зависит от того, какое слагаемое больше - положительное или отрицательное.
7. Произведение двух чисел одного знака положительно, а произведение двух чисел разных знаков отрицательно.
8. Частное двух чисел одного знака положительно, а произведение двух чисел разных знаков отрицательно.
x∈(0; +∞)
Пошаговое объяснение:
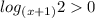
Одз:
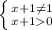
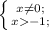
x∈(-1; 0) ∪ (0; +∞)
1) При 0< X + 1 < 1 ⇒ -1 < x < 0;
получаем отрезок:
x∈(-1; 0) (1) он соответствует нашему ОДЗ, можно не вносить правки.
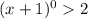(2)
Т.к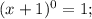 
, а единица всегда меньше 2. То выражение (2) не имеет решения.
2) При X+1 > 1 ⇒ X > 0
получаем отрезок:
x∈(0; +∞) Находим пересечение с ОДЗ, которые мы нашли ранее.
x∈(0; +∞) ∩ x∈(-1; 0) ∪ (0; +∞) = x∈(0; +∞) (3)
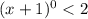(4)
Т.к 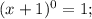, а единица всегда меньше 2. То выражение (4) имеет бесконечное множества решений, x∈(-∞; +∞). Найдя пересечения (3) и (4) :
x∈(0; +∞) ∩ x∈(-∞; +∞) = x∈(0; +∞)
Мы найдем отрезок удовлетворяющий всем условием задания
ответ: x∈(0; +∞)
1 13/35= 48/35
6 5/14=89/14
44/6*48/35=2112/210
2112/210+89/14=3447/210=1149/70