Такие задачи решаются с конца: Пусть в конце игры стало у каждого по 48 рублей. Так как после 4-ой игры проигравший был D, то чтобы выяснить ситуацию по окончании 3-ей игры надо вернуть D половину денег каждого из А, В, С. Имеем: А - 24 рубля, В - 24 рубля, С - 24 рубля и D - 120 рублей.
Аналогично поступаем дальше, теперь возвращаем половину денег от А, В и D игроку С:
А - 12 рублей, В - 12 рублей, С - 108 рублей, D - 60 рублей.
Далее возвращаем половину денег от А, С и D игроку В:
А - 6 рублей, В - 102 рублей, С - 54 рублей, D - 30 рублей.
И наконец возвращаем половину денег от В, С и D игроку А, т.е. возвращаемся к ситуации до игры, это и будет ответ на вопрос задачи:
А - 96 рублей, В - 51 рублей, С - 27 рублей, D - 15 рублей.
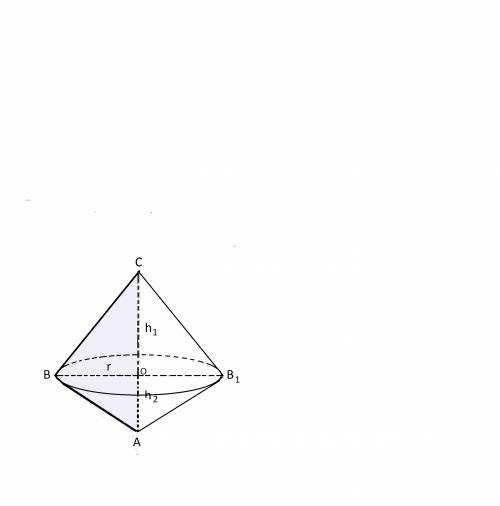
Тело, которое получилось, имеет веретенообразную форму: два конуса с одним общим основанием,
радиус r которого - высота ВО треугольника АВС, проведенная к стороне АС, вокруг которой треугольник вращается;
образующие - АВ и ВС соответственно;
высота каждого конуса - СО и ОА, сумма которых равна АС.
Объем тела вращения равен сумме объемов конусов:
V=v₁ +v₂
v₁=Sh₁:3=πr²h₁:3
v₂=Sh₂:3=πr²h₁:3
V=πr²h₁:3+πr²h₁:3=S(h₁+h₂):3=πr²*АС:3
Радиус r основания, общего для обоих конусов, найдем из площади треугольника АВС, найденной по формуле Герона.
Вычисления банальны, приводить поэтому иx не буду.
Площадь треугольника АВС равна 84
r=ВО=2S ᐃ АВС:АС=168:21=8
V =πr²*АС:3=π*64*21:3=448π
Площадь поверхности равна сумме площадей боковой поверхности конусов:
Sт.вр.=πrL₁+πrL₂=πr(L₁+L₁)
Sт.вр.=π*8*(10+17)=216π
ответ: х=2.