Вывод формулы длины астроиды приведен во вложении.
В задании радиус окружности задан как a.
Если принять начало дуги при t1 = 0, то L = (3/2)a*sin²t.
Длина дуги от 0 до (π/2) равна:
L = (3/2)*a*sin²π/2) = (3/2)*a*1² = 3a/2.
Четвёртая часть её равна 3a/8.
Приравняем 3a/8 = (3/2)a*sin²t.
После сокращения и приведения к общему знаменателю получаем:
1 = 4a*sin²t, отсюда sin²t = 1/4.
После извлечения корня оставляем положительное значение для 1 четверти: sint = 1/2.
Получаем угол для точки М: t = arc sin(1/2) = π/6.
Теперь находим ответ:
x(M) = a*cos³(π/6) = a(√3/2)³ = a*3√3/8.
y(M) = a*sin³(π/6) = a(1/2)³ = a/8.
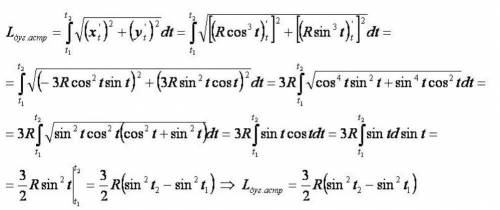
4х =(130-х):3
130-х =4х*3 = 12х
13х = 130
Х = 130:13
Х = 10 (деталей выточил ученик)
130-10=120 (деталей) выточил токарь.
ответ:токарь выточил 120 деталей, ученик 10.