1)(20 1/2+12 3/5)*1/10 = 3,31
1) 20,5 + 12,6 = 33,1
2) 33,1 • 0,1 = 3,31
2)(8 1/4- 2 5/16)*4/25 = 0,85
1) 8 1/4 - 2 5/16 = 8 4/16 - 2 5/16 = 5 15/16
2) 5 15/16 • 4/25 = 95/16 • 4/25 = 17/4 • 1/5 = 17/20 = 0,85
3)(2/7+5/21):1 4/7 = 1/3
1) 2/7 + 5/21 = 6/21 + 5/21 = 11/21
2) 11/21 : 1 4/7 = 11/21 • 7/11 = 1/3
4)(8/11+3/22):5/11 = 1,9
1) 8/11 + 3/22 = 19/22
2) 19/22 • 11/5 = 1/9
5) 1 7/36:(3/8+5/12) = 1 29/57
1) 3/8 + 5/12 = 9/24 + 10/24 = 19/24
2) 1 7/36 • 24/19 = 43/36 • 24/19 = 43/3 • 2/19 = 86/57 = 1 29/57
6) 17/36:(7/12-5/9) = 17
1) 7/12 - 5/9 = 21/36 - 20/36 = 1/36
2) 17/36 • 36/1 = 17
Пошаговое объяснение:
ДАНО: y = 3*x⁷
Вычисляем при х= -1
3*(-1)⁷ = - 3*1⁷ или y(-x) = - y(x) - функция нечётная - ответ.
Дополнение.
Если все члены функции имеют чётные степени - функция чётная.
a*х⁴ + b*x² + c - чётная - симметрия относительно оси ОУ.
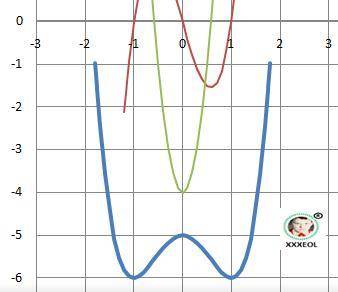
Пример графика с функцией четвертого порядка в приложении.
Если все члены функции имеют нечётные степени - функция нечётная.
a*x⁵ + b*x³ + c*x - нечётная функция - центральная система относительно начала координат О(0;0).
Пример графика нечётной степени в приложении.
А если степени разные - функция общего вида