1)40
2)130
3)53
4)40 и 80
5)120
6)110
Пошаговое объяснение:
1) Угол АОС- центральный, он равен 80 , значит и дуга АС(на которую он опирается ) =80
Угол АВС- не центральный, значит он равен 1\2 АС(дуги на которую опирается )
1\2*80=40
2) Мы имеем четырехугольник, сумма его углов равно 360
Угол ДАВ лежит на дуге ВД и мы видим, что это половина окружности, а вся окружность 360
360\2=180
Угол ДАВ обычный,значит 1\2ВД
1\2*180=90
Аналогично угол ВСД =180*1\2=90
затем 360-90-90-50=130
3)Смотри, АВ проходит через центр и делит окружность на половины, это диаметр. Каждая половина по 180(см задачу 2)
Угол АСВ =1\2*180=90
Сумма углов треугольника 180
180-90-37=53
4)Угол АВД обычный, он лежит на дуге АД
Угол АВД=1\2 АД
Значит АД=2* угол АВД=2*40=80
Дальше, угол АСД тоже лежит на дуге АД и он тоже обычный, значит равен углу АВД и равен 40
Угол АОД центральный, а значит равен дуге , равен 80
5) смотри, угол АОС центральный, а значит дуга равна этому углу ,АС=120
360-120=240 -большая дуга АС
Угол АВС обычный = 1\2 большей дуги АС
АВС=1\2*240 = 120
6) ВСД лежит на дуге ВД, адуга ВД состоит из дуги АД и ВА
АД = 180 , так как АД это диаметр
ВСА обычный угол , значит ВА=2*20=40
Дуга ВД =180+40=220
Угол ВСД обычный
ВСД=1\2*220=110
1. A = {x| x∈N, (x+1)² < 27}
т.к. x - натуральное число, то x≥1, то x+1≥2>0,
(x+1)²< 27
5²=25<27 < 36 = 6²
т.к. x - натуральное, то имеем
0<x+1≤5,
1≤x≤4;
A = {1; 2; 3;4},
|A| = 4;
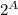 = {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
= {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
{1; 2; 4}, { 1; 3; 4}, {2; 3; 4}, {1; 2; 3; 4}}
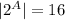
2. A = {0; 1; {2;3}}
B = {1; 2; 3}
C = {5; 6}
C-A = C\A = {5; 6},
A∩C = ∅,
B+C = BΔC = {1; 2; 3; 5; 6},
A - (B∪C) = A\(B∪C) = {0; 1; {2;3}}\{1; 2; 3; 5; 6} = {0; {2; 3}}.
3.
(A∩B)+(A∩C) = (A∩B)Δ(A∩C)

240-60=180 кг осталось после первого дня продаж
180*2/5=72 кг продано во второй день
180-72=108 кг осталось