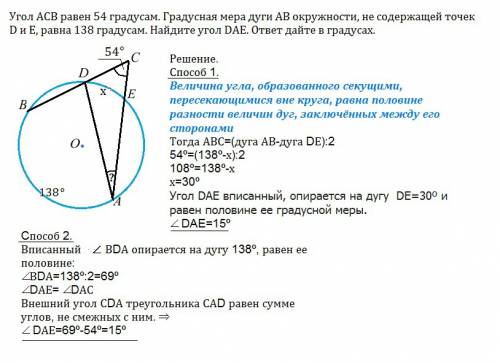
Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
Допустим длина прямоугольника равна Х, тогда ширина равна У .
Начальная формула периметра прямоугольника такова :
Р = 2 ( х+у ) ;
Р = 2х + 2у ;
В задаче дано что длину увеличили на 4 - ( х+4 ) , а ширину уменьшили на 2 - ( у -2 ) ;
Тогда мы получим уже другую формулу периметра :
Р = 2 ((х+4) + (у-2)) ;
Р = 2 ( х + у + 2 ) ;
Р = 2х + 2у +4 ;
Сравнив с первой формулой периметра мы видим , что она отличается от нее на 4 ;
Тоисть можем сделать вывод ,что при таких условиях , которые заданы в задаче периметр прямоугольника увеличится на 4 ;
Здесь синус=0,5, значит квадрат стороны равен10. Периметр 4*sqrt(10).
sqrt(10)-это корень из 10.