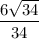
Пошаговое объяснение:
Синус острого угла прямоугольного треугольника - это отношение противолежащего (этому углу) катета к гипотенузе.
Если ∠A = 90° (по условию), то AB и AC - катеты данного треугольника. А BC - гипотенуза.
Противолежащим углу C катетом является AB.
В таком случае sinC = AB/BC. Но чтобы рассчитать синус угла, нужно знать длину гипотенузы.
Если даны длины любых двух сторон прямоугольного треугольника, то длину третьей можно вычислить по теореме Пифагора.
Теорема Пифагора:
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
По условию задачи известно, что AC = 14, AB = 12, тогда по теореме Пифагора:
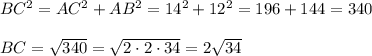
Теперь можем рассчитать sinC:
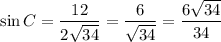
(sinα+cosα)²=(6/5)²
sin²α+2sinα*cosα+cos²α=36/25
1+2sinαcosα=36/25. 2sinα*cosα=36/25-1. 2sinα*cosα=11/25
sinα*cosα=11/50
2. sinα+cosα=1/2
tgα+ctgα=sinα/cosα+cosα/sinα=(sin²α+cos²α)/(sinα*cosα)=1/(sinα*cosα)
sinα+cosα=1/2. (sinα+cosα)²=(1/2)². sin²α+2sinα*cosα+cos²α=1/4
1+2sinα*cosα=1/4. 2sinα*cosα=-3/4. sinα*cosα=-3/8
1:(-3/8)=-8/3
tgα+ctgα=-8/3
3. tgα=2/5. sinα/cosα=2/5. sinα=2cosα/5
(sinα+2cosα)/(cosα-3sinα)=(2cosα/5+2cosα)/(cosα-6cosα/5)=
=[cosα*(2/5+2)] / [cosα*(1-6/5)]=(12/5):(-1/5)=-12
(sinα+2cosα)/(cosα-3sinα)=-12