Сравниваем запись в десятичной и двоичной системе.
1111₁₀ = 1*10³ + 1*10² + 1*10¹ + 1*10⁰ = 10000 + 1000 + 100 + 10 + 1
1111₂ = 1*2³ + 1*2² + 1*2¹ + 1*2⁰ = 8 + 4 + 2 + 1 = 15₁₀.
Видим, что для записи двузначного десятичного числа 15 понадобилось четыре разряда в двоичной системе.
Примеры записи чисел: 10₂ = 1*2¹+ 0*2⁰ = 2₁₀ и 100₂ = 1*2² + 0*2¹ + 0*2⁰ = 4₁₀ и
101₂ = 1*2² + 1*2⁰ = 4 + 1 = 5₁₀ и 110₂ = 2² + 2¹ = 4 + 2 = 6₁₀ и 1110₂ = 2³+2²+2¹ = 8 + 4 + 2 = 14₁₀
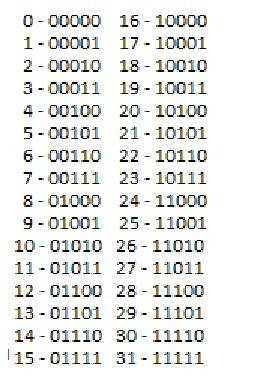
На рисунке в приложении показана запись натуральных чисел от 0 до 31 в двоичной системе исчисления.
В чём же преимущество двоичной системы - в её простоте. В каждом разряде всего два значения - 0 и 1. Недостаток - большое число разрядов для записи числа. Но эту проблему легко решают современные процессоры. Каждый разряд в двоичной системе называется - бит. Число в 32 бит (это 32 единицы в записи) соответствует десятичному числу = 4 294 967 296 , а процессоры в 64 бит могут работать с числами до 1,8*10¹⁹ (19 нулей после запятой). Всего две цифры открывают безграничные возможности.
тогда 2х/5 - засушили
х-2х/5 - осталось после сушения
(х-2х/5)*5/9 - засолили
Зная, остаток составляет 28 штук, составим уравнение:
х-2х/5-(х-2х/5)*5/9=28
х-2х/5-((5х-2х)/5)*5/9=28
х-2х/5-3х/9=28
Приведем к общему знаменателю левую часть уравнения
(45х-18х-15х):45=28
12х=28*45
12х=1260
х=105 (грибов) - всего собрали
(105:5)*2=42 (гриба) - засушили
105-42=63 (гриба) - осталось после сушения
(63:9)*5=35 (грибов) - засолили
Проверка: 42+35+28=105 (грибов) - собрали всего
Определим какую часть от собранных составляют засоленные грибы:
105:35=3. Т. е это 1/3 часть.
ответ: всего собрали 105 грибов, а засолили 1/3 часть от собранных грибов