Поехали:
Как обычно, начинаем с ОДЗ:
х > 0
х ≠ 0,5
х < 3
х ≠ 3/2
Таким образом наша ОДЗ:
(0;0,5) ∪(1/2; 3/2) ∪ (1,5;3)
Идем к уравнению. Приводим все к основанию 2:
![\frac{\frac{log(2)[4x^{2}] }{log(2)[16]}-\frac{log(2)[\frac{x}{2} }{log(2)[(2x)^{\frac{1}{2} }] } }{\frac{4log(2)[1-\frac{x}{3}] }{log(2)[16]}+1 }\frac{log(2)[x]}{log(2)[2-\frac{2}{3}x] }](/tpl/images/1058/3710/fda95.png)
Переносим всё в одну сторону, ищем общий знаменатель, производим действия типа log(2)[16] = 4:
![\frac{\frac{1+log(2)[x]}{2}-\frac{2(log(2)[x-1])}{log(2)[x]+1}-log(2)[x] }{log(2)[1-\frac{x}{3}]+1 }0](/tpl/images/1058/3710/b40b4.png)
![\frac{1-log(2)[x]}{log(2)[1-\frac{x}{3}]+1 }(\frac{1}{2}+\frac{2}{log(2)[x]+1}) 0](/tpl/images/1058/3710/2465f.png)
![\frac{(1-log(2)[x])(log(2)[x]+5)}{(log(2)[x]+1)(log(2)[1-\frac{x}{3}] +1)} 0](/tpl/images/1058/3710/9f0b0.png)
![\frac{(log(2)[x]-1)(log(2)[x]+5)}{(log(2)[x]+1)(log(2)[1-\frac{x}{3}] +1)} < 0](/tpl/images/1058/3710/d8a7d.png)
Методом интервалов:
- + - + -
___________₀________₀________₀________₀_________
1/32 1/2 3/2 2
/////////////////// /////////////// ////////////////////
( - ∞ 1/32) ∪ (1/2; 3/2) ∪ (2; + ∞)
Подводим к нашему ОДЗ:
/////////////////////////////////////////////////////////////////////////////
____₀_______₀________₀________₀________₀______₀__________
0 1/32 1/2 3/2 2 3
/////////////////// /////////////// ////////////////////
Таким образом получаем:
х ∈ (0; 1/32) ∪ (1/2 ; 3/2) ∪ (2 ; 3)
ответ: х ∈ (0; 1/32) ∪ (1/2 ; 3/2) ∪ (2 ; 3)Пусть уравнения прямых имеют вид:
l₁:y=k₁x+m₁
l₂:y=k₂x+m₂
Прямые проходят через точку (5;25)
Подставим координаты точки в уравнения:
25=5k₁+m₁ ⇒m₁ =25-5k₁
25=5k₂+m₂ ⇒m₂=25-5k₂
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1):
k₁k₂=-1
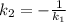
Пусть k₁=k, тогда 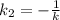
По условию: прямая l₁ пересекает ось Ox в точке (a;0)
Подставляем координаты точки в уравнение l₁:y=kx+ 25-5k
0=ka+25-5k
и пересекает график функции y=x² в точке (b;b²).
Подставляем координаты точки в уравнение l₁:y=kx+ 25-5k
b²=kb+25-5k
Прямая l₂ пересекает ось Ox в точке (c;0)
Подставляем координаты точки в уравнение l₂: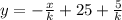
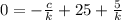
и пересекает график функции y=x² в точке (d;d²)
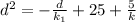
Получаем систему:
{0=ka+25-5k
{b²=kb+25-5k
{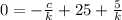
{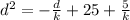
Перепишем:
{ka=5k-25
{kb=b²-25+5k
{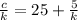
{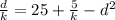
перемножаем:
abcd=
Через 1 час останется
1 - (1/3 + 1/4) = 1 - 7/12 = 5/12 всего расстояния - ОТВЕТ