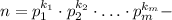разложение n на простые множители. Каждый делитель числа n имеет подобный вид с теми же основаниями и с показателями от 0 до степени, в которую это простое число входит в разложение числа n. Поэтому n имеет 
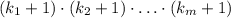делителей. Но по условию n имеет 15 делителей. Это приводит к двум случаям.
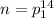. Этот случай нас не устраивает, так как это число больше, чем 300.
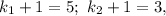то есть 
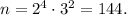
и так далее, больше, чем 300.
2(8+7)=30 периметр