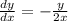
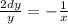 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными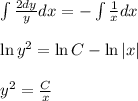
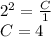
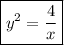 - частный интеграл.
- частный интеграл.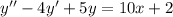
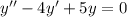
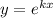 , тогда получаем
, тогда получаем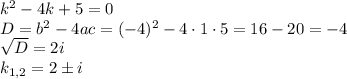
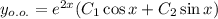
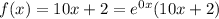
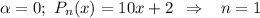
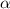 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: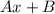
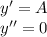
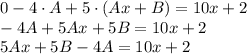
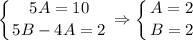
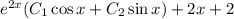
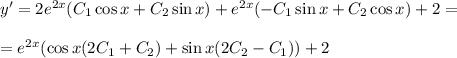
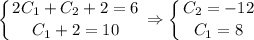
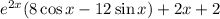
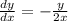
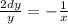 - уравнение с разделёнными переменными
- уравнение с разделёнными переменными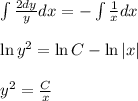
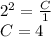
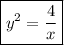 - частный интеграл.
- частный интеграл.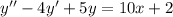
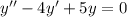
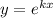 , тогда получаем
, тогда получаем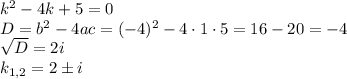
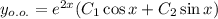
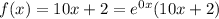
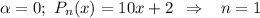
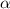 с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде:
с корнями характеристического уравнения и принимаем во внимания что n=1, то частное решением будем искать в виде: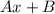
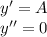
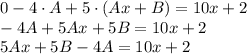
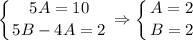
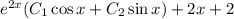
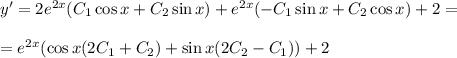
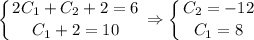
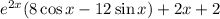
2)419-140=279
1)6*70=420
2)420-285=195
1)140-80=60
2)80*60=4800
3)4800+570=5370
1)80*20=1600
2)1600+769=2369
3)2369-684=1685
1)720:9=80
2)576+80=656
3)656-578=78