Нужно найти вероятность события - Р(А).
Р(А) - это вероятность того, что после трех бросков монеты герб выпадет хотя бы один раз (это может быть и один, и два, и три раза).
Сначала нужно определить число возможных исходов - m.
Затем определить число благоприятных исходов (того, что герб выпадет хотя бы один раз) - n.
По формуле определяем вероятность нужного нам события Р(А)=n/m.
После трех бросков монеты возможны 8 исходов: ГГГ (3 раза выпадет герб); ГРР (один раз - герб; два раза - решка); ГГР; ГРГ; РРР; РГГ; РРГ; РГР; m=8.
Из них благоприятных исходов - 7 (герб не выпадает только в одном исходе РРР); n=7.
Р(А)=n/m=7/8.
ответ: 7/8
1) Если учитывать все возможные числа от 01 до 99, то вероятность p ≈ 0,056
2) Если учитывать все возможные числа от 10 до 99, то вероятность p ≈ 0,062
Пошаговое объяснение:
Вероятность равна отношению благоприятных исходов (m) к общему количеству попыток (n).
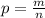
Из множества чисел от 0 до 99 делятся на 18 следующие:
18; 36; 54; 72; 90.
Итого благоприятных исходов m = 5.
Найдем общее количество двузначных чисел, удовлетворяющих условию задачи.
Так как карточек с числами всего 10, по одной цифре от 0 до 9, то мы не можем составить числа вида 11; 22; ...; 99. Т.е. 9 чисел из числа двузначных нужно исключить.
1) Если к двузначным числам отнести составленные из двух карточек числа вида 01; 02 и т.д. (т.е. числа с незначащим нулем впереди), то всех двузначных чисел будет n = 99 - 9 = 90.
Тогда вероятность 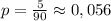
2) Если к двузначным числам мы не относим числа вида 01; 02; ...; 09, то всех двузначных чисел будет n = 99 - 9 - 9 = 81.
Тогда вероятность 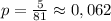 .
.
2х - во 2 бригаде.
х + 2х+5 - в 3 бригаде.
х + 2х + х + 2х + 5 = 215
6х = 215 -5
6х = 210
х = 35 чел. - в 1 бригаде.
2 * 35 = 70 чел. = во 2 бригаде.
35 + 70 +5 = 110 чел. - в 3 бригаде.