448 дм²
Пошаговое объяснение:
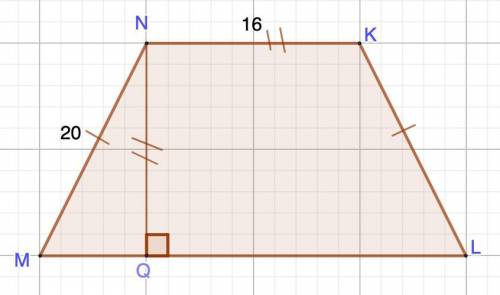
Дано: MNKL - равнобедренная трапеция
NQ = NK;
MN=20 дм, NK= 16 дм.
Найти: S - площадь трапеции.
Рассмотрим ΔMNQ.
MN=20 дм, NQ = NK = 16 дм.
По теореме Пифагора:
MQ² = MN² - NQ² =400 - 256 = 144
⇒ MQ = √144 = 12 (дм)
Высота, опущенная из вершины тупого угла равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований.⇒MQ = (ML - NK):2
12 = (ML - 16) : 2
ML - 16 = 24
ML = 40 (дм)
Площадь трапеции равна произведению полусуммы оснований на высоту.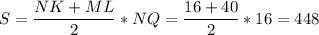 (дм²)
(дм²)
3/5 = 21/35, 15/35 ⇒ 3/5 > 3/7,
б)
3/8 = 9/24, 7/3 = 56/24 ⇒ 3/8 < 7/3,
в)
5/8 = 45/72, 7/9 = 56/72 ⇒ 5/8 < 7/9