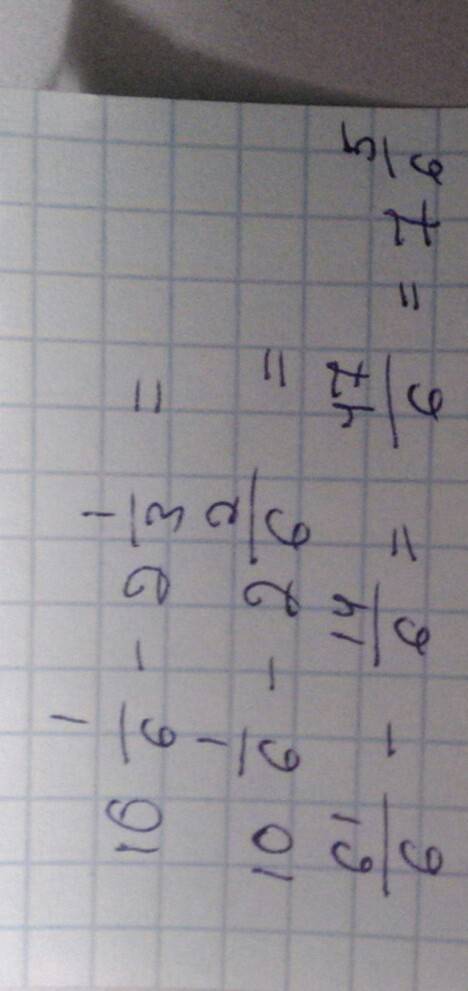
Найдём уравнение прямой М1М2, проходящей через точку М1(-5;-15;-6) с направляющим вектором s = (0; 5; 2).
(x + 5)/0 = (y + 15)/5 = (z+ 6)/2 = t.
Уравнение М1М2 представим в параметрическом виде.
x = 0t - 5,
y = 5t - 15,
z = 2t - 6.
И подставим в уравнение плоскости Р: 7x-3y+5z-10=0.
-35 - 15t + 45 + 10t - 30 - 10 = 0.
-5t - 30 = 0
t = -30/-5 = 6.
Получаем координаты точки М2 пересечения прямой М1М2 с плоскостью Р.
x = 0*6 - 5 = -5,
y = 5*6 - 15 = 15,
z = 2*6 - 6 = 6.
Точка М2(-5; 15; 6).
Составим уравнение плоскости, проходящей через точки M1(-5;-15; -6), М2(-5; 15; 6) перпендикулярно плоскости Р: 7x-3y+5z-10=0.
Так как M1 ∈ Р, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x+5)+B(y+15)+C(z+6)=0.
Далее, так как M2 ∈ Р, то подставив координаты точки в выписанное уравнение, получим равенство: A(-5+5)+B(15+15)+C(6+6)=0
0A + 30В + 12C = 0 или 30В + 12C = 0. Отсюда С = (-30/12)В = (-5/2)B.
Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.
Выразим коэффициенты A и С через В:
Составим систему уравнений:
{ A + B + C = 0. { A + B + C = 0.
{A + 30В +12(-5/2)В = 0. {A + 30В - 30В = 0, A = 0.
A = 0, С = (-5/2)B и подставим их в исходное уравнение:
A(x+5) + B(y+15) + C(z+6) = 0.
0 + B(y+15) + (-5/2)B(z+6 )= 0, сократим на В:
y + 15 + (-5/2)z - 15 = 0, приведём к общему знаменателю:
2y + 30 - 5z - 30 = 0.
Окончательно получаем уравнение плоскости Р1: 2y - 5z = 0.
Расстояние от точки M(x0,y0,z0) до плоскости P1:Ax+By+Cz+D=0 вычисляется по формуле
d = ∣Ax0+By0+Cz0+D|/√(A²+B²+C²).
Подставляем:
d = |0*5 + 2*14 + (-5)*3|/√(0² + 2² + (-5)²) = 7/√29 ≈ 1,3.
Пошаговое объяснение:
Карточка 1.
21,5; 22; 22,5; 23; 23
Объем = 5
х = (22,5 + 23 +21,5 + 22 + 23) : 5 = 112:5 = 22,4 - среднее арифметическое
R = 23 - 21,5 = 14,5 - размах
Мо = 23 - мода
Ме = 22,5 - медиана
Карточка 2.
-4; -3; -2; -2; 3; 3; 3; 5; 6
Объем = 9
Х = (6 - 4 + 5 - 2 - 3 + 3 + 3 - 2 + 3) : 9 = 9 : 9 = 1 - среднее арифметическое
R = 6 - (-4) = 6+4 = 10 - размах
Мо = 3 - мода
Ме = 3 - медиана
Карточка 3.
12; 12; 12,5; 12,5; 12,5; 13; 13
Объем = 7
Х = (12,5 + 12 + 12 + 12,5 + 13 + 12,5 + 13) : 7 = 78,5 : 7 = 12,5
R = 13 - 12 = 1
Мо = 12,5
Ме = 12,5
Карточка 4.
-1; -1; -1; 0; 0; 1; 2; 2
Объем = 8
Х = (-1 + 0 + 2 + 1 - 1 + 0 + 2 - 1) : 8 = 2 : 8 = 0,25
R = 2 - (-1) = 2+1 = 3
Мо = -1
Ме = 0
Карточка 5.
124; 125; 130; 131
Объем = 4
Х =(125 + 130 + 124 + 131) : 4 = 510 : 4 = 127,5
R = 131 - 124 = 7
Мо - нет
Ме = (125+130):2 = 255:2 = 127,5
Карточка 6.
100; 110; 120
Объем = 3
Х = (120 + 100 + 110) : 3 = 330: 3 = 110
R = 120-100 = 20
Мо - нет
Ме = 110