Пошаговое объяснение:
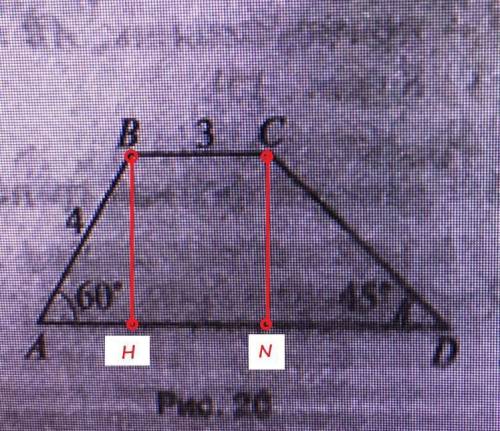
Проведем высоту ВН. Получим треугольник АВН, у которого угол АВН=30*. Тогда АН=1/2АВ=4*1/2=2.
Найдем высоту ВН.
ВН^2=FD^2-AH^2=4^2-2^2=16-4=12;
BH=√12=2√3.
Проведем высоту CN. Получим треугольник CDN, у которого угол CDN равен углу NCD и равен 45*. Следовательно треугольник CDN - равнобедренный и CN=DN. Но CN=BH=√12. Следовательно DN=CN=BH=√12=2√3.
Основание AD=AH+HN+ND=2+3+√12=5+√12.
Найдем сторону CD. CD^2=CN^2+DN^2=(√12)^2+(√12)^2=12+12=24;
CD=√24=2√6.
Периметр P(ABCD)=AB+BC+СD+AD=4+3+2√6+5+√12=2√3+2√6+12.
Площадь S(ABCD)=BH*(AD+BC)/2=2√3(5+2√3+3)/2=8√3+6.
См. скриншот.
Пошаговое объяснение:
1.
а) (1,5 * 3,1) - 2,63 = 4,65 - 2,63 = 2,02
б)
1) 45 : 3. 6/13 = 45 : 45/13 = 45 * 13/45 = 1*13/1 = 13/1 = 13
2) 13 - 13,06 + 1. 3/8 = -0,6 + 11/8 = -0,6 + 1,375 = 0,775
2.
а)
2,5у = 25,6 - 0,65
2,5у = 24,95
у = 24,95 : 2,5
у = 9,98
б)
х = 1. 1/3*4,7 / 5. 2/9
х = 1. 1/3 * 4. 4/10 / 5. 2/9
х = 4/3 * 44/10 / 47/9
х = 1/3 * 11/10 / 47/9
х = 11/30 : 47/9
х = 11/30 * 9/47
х = 11/10 * 3/47
х = 33/470
6.
Найдём расстояние между Х и Y :
12 - (-21) = 12 + 21 = 33 см
33 : 3 = 11 см - каждый отрезок.
Найдём координаты :
ХМ = -21 + 11 = -10 (координата точки М)
МN = -10 + 11 = 1 (координата точки N)
а) 3/2= 1 1/2
б) 125/126
Пошаговое объяснение:
Для нача сокращаем 84/48 на 2 получаем 21/12, потом сокращаем 108/126 на 2, потом на 9 и получаем 6/7. Потом умножаем 21/12 на 6/7 и получаем ответ.
Второй решаем по тому же принципу