1) По формуле сложения сворачиваем, получается:
cos (128+52)=cos 180= -1
2) Я, так понимаю, косинус найти нужно?
Если так, то:
применяем основную тригонометрическую формулу sin^2 x+cos^2 x =1, подставляем все известные и решаем:
cos^2 x=1-(144/169)
cos^2 x=25/169
cosx = 5/13, но поскольку косинус во 2 четверти отрицательный, то ответ -5/13
3)2sin+sqrt2 = 0 (sqrt - корень)
2sin = -sqrt2
sin = -sqrt2/2
x=(-1)^k+1 * 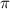 /4+2
/4+2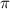 n, n
n, n  z
z
4) tg^2 x - tgx = 0
Выносим tgx за скобку:
tgx(tgx-1)=0
tgx=0 tgx-1=0
x = 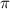 n, n
n, n  z tgx=1
z tgx=1
x=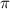 /4+
/4+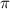 n, n
n, n  z
z
Y = -x³ + 48х
1. Корни функции
Y=0 при Х₁ = - 4, Х₂ = 0, Х₃ = 4
2. Производная функции
Y'(x) = - 3x² + 48
3. Корни производной
Y'(x)= 0
X₁ = - 2,3, Х₂ = 2,3.
3. Экстремумы функции
Ymin(-2,3) = - 73,9
Ymax(2.3) = 73,9
4 Промежутки монотонности.
Убывает - Х∈(-∞;-2.3]∪[2.3+∞)
Возрастает - Х∈[-2.3;2.3]
5. Вторая производная.
Y"(x) = - 6*x²
6. Точка перегиба - Y"(x)=0 при X = 0.
7. Вогнутая - "ложка" - Х∈(-∞;0]
выпуклая - "горка" - X∈[0;+∞)