Question

20 б.

в параллелограмма abcd высота bh = 12 см проведена к стороне ad, диагонали ac = 15 см, bd = 13 см. найдите площадь параллелограмма

Answer 1

84 см²

Пошаговое объяснение:

Площадь параллелограмма: S=h*a,

где а- длина основания, h-высота.

В нашей задаче известна высота: h=BH=12 см.

Найдём длину основания.

Меньшая и большая* диагонали образуют с высотой два прямоугольных треугольника, где высота выступает катетом, а диагональ - гипотенузой.

*Прямоугольный ΔВНС' получаем путём сдвига большей диагонали АС на точку Н, и получаем НС'.

Найдем неизвестные катеты:

$HD=\sqrt{BD^{2}-BH^{2} } =\sqrt{169-144} =\sqrt{25}=5$

BC'=$\sqrt{AC^{2} -BH^{2} } =\sqrt{225-144} =\sqrt{81}=9$

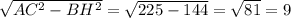
Половина суммы длин этих катетов равна длине основания.

Докажем это утверждение. Обозначим основание BC=AD за х, а отрезок АН за а. Тогда НD=х-а, ВC'=x+a. Следовательно HD+BC'=2x и искомое основание х равно половине этой суммы.

(HD+BC')/2=7 см

Тогда площадь АВСD=12*7=84 см²