![\lim_{x \to 1} \dfrac{x^3 - x^2 - x + 1}{x^3 - 3x + 2 } = \lim_{x \to 1} \dfrac{x^2(x - 1) - (x - 1)}{x^3 - x^2 + x^2 - x - 2x + 2 } = \\ \\ \lim_{x \to 1} \dfrac{(x - 1)(x^2 - 1)}{x^2(x - 1) + x(x - 1) - 2(x - 1) } = \\ \\ \lim_{x \to 1} \dfrac{(x - 1)(x - 1)(x + 1)}{(x - 1)(x^2 + x - 2) } = \lim_{x \to 1} \dfrac{(x - 1)(x - 1)(x + 1)}{(x - 1)(x^2 -x + 2x - 2) } = \\ \\ \lim_{x \to 1} \dfrac{(x - 1)(x - 1)(x + 1)}{(x - 1)[x(x - 1) + 2(x - 1)] } = ](/tpl/images/0785/3012/d6dc5.png)
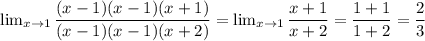
Пошаговое объяснение:
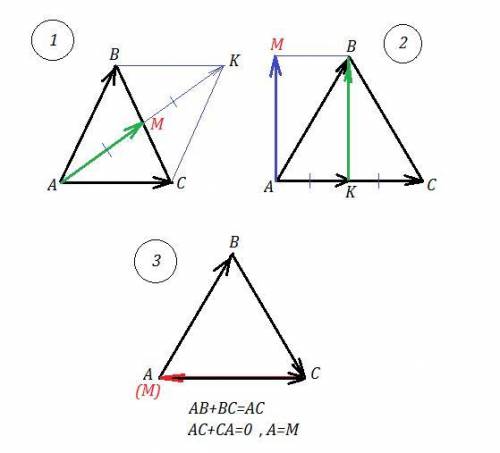
1) АМ - вектор, равный половине вектора АК, АК=АВ+АС .
Складываем векторы по правилу параллелограмма.
Точка М - середина диагоналей параллелограмма АВКС, точка их пересечения. Смотри рис. 1.
2) 1/2*АС - это вектор АК ; АВ-1/2*АС=АВ-АК=КВ
Теперь выполним параллельный перенос вектора КВ, точку К совместим с точкой А, тогда точка В перейдёт в точку М. Смотри рис. 2.
3) Пользуемся правилом треугольника сложения векторов: АВ+ВС=АС.
Теперь к АС нужно прибавить такой вектор, чтобы получить нулевой вектор. Его длина должна быть равна 0, а начало нулевого вектора совпадает с его концом. Но АС-СА=0, то есть в качестве вектора СМ надо взять вектор СА. Точка М совпадает с точкой А .
АВ+ВС+СМ=0. Смотри рис. 3.
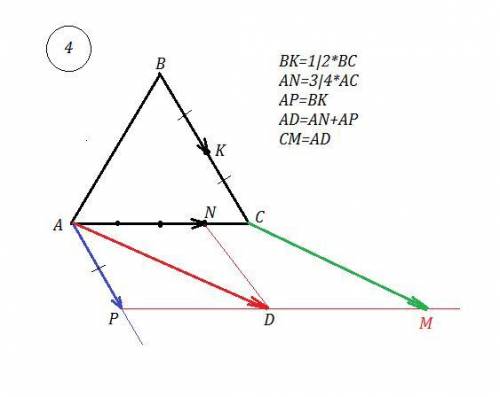
4) 4*СМ=3*АС+2*ВС ⇒ СМ=3/4*АС+2/4*ВС=3/4*АС+1/2*ВС
ВК=1/2*ВС , АР=3/4*АС
Выполним параллельный перенос вектора ВК , совместив точку В с точкой А, получим вектор АР=ВК.
Сложим по правилу параллелограмма АК+АР=AD .
Выполним параллельный перенос вектора AD так, чтобы точка А совпала с точкой С. Тогда точка D перейдёт в точку М. Получим вектор СМ=АР. Смотри рис. 4.