На одной полке стояло х книг,а на второй-в 4 раза больше.когда со второй полки переставили на первую 21 книгу,то книг на полках стало поровну.запишите выражения для следующих величин: 1.число книг на второй полке первоначально 2.число книг на второй полке после того,как оттуда убрали 21 книгу 3.число книг на первой полке после того ,как туда поставили 21 книгу найдите равные величины и составьте уравнение- модель данной ситуации.

 - Диагональ параллелепипеда.
- Диагональ параллелепипеда.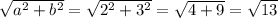 - Её диагональ.
- Её диагональ.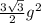 , где g - сторона основания.
, где g - сторона основания. - Большая диагональ основания
- Большая диагональ основания .
. - длина стороны основания.
- длина стороны основания.
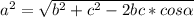
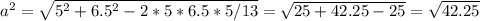 =6.5.
=6.5.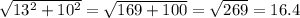
х+21-4х+21=0
-3х+42=0
Х=14 было на первой
14•4 = 56 было изначально на второй
56-21=35 стало на второй